Горелик Г. Е.,
Френкель В. Я.
Матвей Петрович
Бронштейн: 1906—1938.
М. : Наука.
1990. —272 с., ил.
Глава 5. cGћ-физика в биографии Бронштейна
5. 1. Недиссертабельная диссертация
5. 2. Корни интереса к сGћ-физике
а) Квантовая гравитация до Бронштейна.
б) «Отношение физических теорий друг к другу и к космологической проблеме».
в) У истоков квантово-релятивистской астрофизики.
5. 3. Квантовая теория слабого гравитационного поля
в) Планковские масштабы в cGћ-физике.
г) Восприятие квантово-гравитационных границ.
б) Отношение М. П. Бронштейна к космологии.
в) Красное смещение, принцип относительности и поляризация вакуума.
Расскажем теперь о работах Бронштейна, которым суждено было стать главным его вкладом в науку. Это его работы в области теории гравитации и космологии. Наиболее известны результаты его диссертации 1935 г. «Квантование гравитационных волн».
5. 1. Недиссертабельная диссертация
Квантовая теория гравитации как тема исследования и как тема докторской диссертации Бронштейна в 1935 г. могла вызвать недоумение сразу по нескольким причинам. Прежде всего проблему эту тогда никак нельзя было назвать актуальной. Эйнштейн и немногие его единомышленники стремились получить квантовые законы из единой теории поля, обобщающей ОТО. За этим исключением, фундаментальная физика почти целиком была поглощена теорией ядра и квантовой электродинамикой. Этих теорий настоятельно требовала область явлений, позже названная физикой элементарных частиц. А гравитация, как показывали простейшие оценки, для этой области значения не имела. Так что тема, выбранная Бронштейном для диссертации, была в 30-е годы весьма изолированной.
Впрочем, трудно говорить и об актуальности самой ОТО в период ее создания. Конечно, для возникновения ОТО причины имелись, и причины глубокие, но они были внутренними: все они относились к внутреннему несовершенству предшествующей теории [127]. А по внешним, количественным эффектам релятивистская теория гравитации была несравнима с ньютоновским всемирным тяготением и другими фундаментальными теориями в периоды их возникновения. Еще меньшей была практическая потребность в квантовой теории гравитации. История физики, однако, хорошо знает, к каким грандиозным практическим по-
134
следствиям приводят теории, потребность в которых вначале испытывают только немногие теоретики.
В этой книге уже употреблялись названия, сделанные из фундаментальных констант, органически присущих соответствующей теории, явлению и т. д. Ньютоновскую теорию тяготения можно называть G-теорией, ОТО — cG-теорией, а квантовую теорию гравитации — cGћ-теорией. Эти обозначения, как мы увидим, восходят к Бронштейну, и они не просто экономят место, а помогают лучше видеть структуру теоретической физики.
Что касается cGћ-темы для диссертации, то в 30-е годы не только практически, но и принципиально квантование гравитации не обещало ничего нового. Во всяком случае крупнейшие квантовые авторитеты Паули и Гейзенберг в 1929 г., излагая общую схему квантовой электродинамики, заявили безо всяких оговорок: «Следует еще упомянуть, что квантование гравитационного поля, которое необходимо в силу некоторых физических причин, проводится без каких-либо новых трудностей с помощью формализма, вполне аналогичного развитому здесь» [159, с. 32]. Важная оговорка была, конечно, необходима. Фактически Паули и Гейзенберг подразумевали, что квантованию подвергается слабое гравитационное поле, для описания которого достаточны линеаризованные уравнения Эйнштейна. Именно так подошел к квантованию гравитации Л. Розенфельд в 1930 г. [259]. Такой заведомо приближенный подход хотя и позволял надеяться на аналогию с электромагнетизмом, но давал повод забыть об особых свойствах гравитации, связанных с принципом эквивалентности, с геометрическим характером и нелинейностью этого поля. Только Бронштейн обнаружил принципиальную сложность квантования гравитации. А современник, не подозревающий об этом, вряд ли счел бы тему его диссертации перспективной.
Тот же современник, если он участвовал в жизни Физтеха, с не меньшим недоумением отнесся бы к тому, что тема диссертации не связана с физикой полупроводников (перспективность которой не вызывала сомнений). Потому что результаты Бронштейна в этой области были тогда хорошо известны. Их высоко оценивал директор ЛФТИ А. Ф. Иоффе [193]. Заведующий теоротделом Я. И. Френкель в отзыве о Бронштейне даже писал: «В настоящее время им уже факти-
135
чески написана докторская диссертация (на тему об электронных полупроводниках), которую он будет защищать в недалеком будущем» [173, с. 322]. И ученый совет ЛФТИ, присвоив Бронштейну кандидатскую степень за работы по астрофизике без защиты на заседании 10 июня 1935 г., предложил ему представить докторскую диссертацию «Теория полупроводников». В этих обстоятельствах выбрать совсем другую (можно сказать, противоположную) тему — поступок недиссертабельный, или, если не пользоваться нынешним жаргоном, неблагоразумный. Однако степенное благоразумие не было главным качеством Матвея Петровича: кроме того, разве интересно возвращаться к работе трехлетней давности?
И, наконец, тому современнику, который с нашей помощью не устает удивляться теме бронштейновской диссертации, осталось спросить, почему эта диссертация понадобилась вообще. Ведь тогда нередко докторские степени присваивались без защиты диссертации, а в советской теоретической физике Бронштейн был достаточно заметен.
Поясним кое-что для тех, кто не знает, что до 1934 г. в СССР ученых степеней не было. Революция, демократизируя общественную жизнь, отменила разные табели о рангах, в частности обычные воинские звания и ученые степени. В науке дисциплина и надежность управления не имеют такого значения, как в армии, здесь важнее гибкость структуры и свободная инициатива. Стремление измерять научный уровень диссертациями и обозначать ранг научного работника «звездочками на погонах» подвергается сомнению и в наше время. А в 30-е годы у молодых, активно работающих физиков степенная иерархия вызывала еще больший скепсис: в научном сообществе безо всяких степеней становится известен истинный потенциал каждого. Однако административные преимущества системы званий в условиях планирования науки перевесили, и в январе 1934 г. было принято решение «в целях поощрения научной работы и повышения квалификации научных и научно-педагогических кадров» ввести (в течение двух лет) степени кандидата и доктора наук1.
1 В дореволюционной России ученых степеней было три: кандидат, магистр и доктор. Магистерская диссертация соответ ствовала теперешней кандидатской и защищалась после сдачи магистерских (весьма сложных) экзаменов.
136
Чтобы новый механизм заработал, нужно было некоторое начальное количество докторов. Право присваивать ученые степени без защиты диссертации имели ВАК, Президиум АН СССР. Помимо членов Академии докторские степени получили и некоторые физики бронштейновского поколения, например Ландау и Шубин. В том, что Бронштейну пришлось защищать диссертацию, не следует видеть сомнение коллег в его докторском потенциале. Просто система присвоения степеней никогда не была особенно стройной, и, кроме таланта и достижений, учитывались также и другие обстоятельства: и занимаемая должность, и концентрация квалифицированных физиков в окружении. Для Ландау и Шубина, переехавших из научных центров Ленинграда и Москвы в только что организованные в Харькове и Свердловске УФТИ и УрФТИ и ставших там заведующими теоротделов, эти обстоятельства были в плюсе, для Бронштейна — в минусе.
По причинам, вполне понятным, молодые физики, действительно заслуживающие научных степеней, относились к диссертациям без почтения; ведь это отвлекало от настоящей научной работы. Поэтому руководителям ЛФТИ приходилось настойчиво побуждать «неостепенившихся», чтобы они своевременно (до конца 1935 г. ) оформили свои работы в виде диссертаций. По свидетельству И. К. Кикоина, получив очередную взбучку по этому поводу от А. Ф. Иоффе, Матвей Петрович объяснял, что не хочет готовить полупроводниковую диссертацию, потому что в докторской диссертации обязательно должны быть длинные непонятные формулы. Тут, конечно, и красное словцо, но, вероятно, и свидетельство уже определившейся темы: в квантовании гравитации, где кроме десяти потенциалов (метрики) участвуют десять импульсов, без сложных формул не обойтись. (Помня обещание М. П. насытить свою диссертацию сложными формулами, Кикоин принес на защиту подзорную трубу, чтобы не пропустить на доске ни одного, даже самого маленького индекса.)
Диссертационную работу Бронштейн сделал за летние месяцы 1935 г. 10 июня ученый совет был еще уверен, что тема диссертации — теория полупроводников, а августом уже датирована статья [30] с изложением квантово-гравитационных результатов.
137
Защита состоялась 22 ноября 1935 г. Оппонентами выступали два крупнейших советских теоретика — В. А. Фок и И. Е. Тамм. Они высоко оценили работу младшего коллеги, квалификация которого, впрочем, была им хорошо известна и до диссертации. Сохранившаяся стенограмма защиты [173, с. 317—320] и — еще больше — воспоминания очевидцев свидетельствуют, что поведение диссертанта было не очень-то диссертабельным. Он не «защищался», а рассказывал об очередной своей работе.
Какой же путь привел М. П. Бронштейна к теме его диссертационной работы?
Самостоятельным исследователем он был уже в студенческие годы, поэтому напрасно искать, кто бы мог дать ему тему диссертации. Скорее, наоборот. Его «непосредственный начальник», заведующий теоротделом ЛФТИ Я. И. Френкель, относился к квантованию гравитации весьма скептически. Это ясно показывает рукопись статьи «Принцип причинности и полевая теория материи» (Личный архив В. Я. Френкеля), которую Я. И. Френкель подготовил для сборника, посвященного Эйнштейну и вышедшего в США в 1949 г. Вопросу квантования гравитации в этой статье уделен почти целиком параграф «Ядерное и гравитационное поля». Автор анализирует точку зрения, согласно которой гравитационное поле, «или во всяком случае та (слабая) часть его, которая образует гравитационные волны, может быть квантована, чему должно соответствовать появление соответствующих частиц — гравитационных квантов, или гравитонов» и указывает: «А. Эйнштейн был, вероятно, первым, кто указал на связь между гравитационными волнами и соответствующими частицами (в беседе с автором в 1925 г. ). Подробное математическое исследование этого вопроса было опубликовано в нашей стране М. Бронштейном в 1936 г. Результаты Бронштейна недавно развил Д. Д. Иваненко».
Однако Я. И. Френкель выразил несогласие с такой точкой зрения, считая аналогию между гравитационным и электромагнитным полями весьма поверхностной. Его аргументы состояли в том, что «электромагнитное поле представляет собой материю», а гравитационное лишь определяет метрические свойства пространственно-временной протяженности; что, «строго говоря, таких вещей, как гравитационная энергия или
138
импульс, не существует, так как соответствующие им величины не образуют настоящего тензора, а являются лишь псевдотензором» (в этом же Я. И. Френкель видит причину неудач многих попыток сведения теории обоих полей в единую теорию поля). Попытки квантовать гравитацию он считает бессмысленными, поскольку «гравитационное поле имеет макроскопический, а не микроскопический смысл, обусловливая лишь некоторую рамку для описания физических событий в пространстве и времени, тогда как квантование относится лишь к микроскопическим процессам в материальных полях».
Все эти соображения, по существу, не зависели от событий, происшедших после бронштейновской диссертации, и поэтому, а также судя по реплике Френкеля на защите [173, с. 319], можно думать, что его позиция была такой же и в 1935 г.
Отсюда мы, во-первых, еще раз получаем представление о свободной научной атмосфере, характерной для теоротдела ЛФТИ. А во-вторых, убеждаемся, что квантование гравитации вовсе не было само собой разумеющейся, почти технической темой, терпеливо дожидавшейся, пока дойдут до нее руки у теоретиков, исчерпавших темы, более интересные и значительные.
Я. И. Френкель — отнюдь не случайная фигура в области эйнштейновской теории гравитации. Ему, в частности, принадлежит первая в нашей стране книга с изложением ОТО [289]. Для этой книги характерна приверженность к своеобразной электромагнитной картине мира [130]. Но в отношении Френкеля к квантованию гравитации проявилась не только эта приверженность. Сомнения в синтезе квантовых и общерелятивистских идей вызывались особой — геометрической — природой гравитационного поля, отождествлением его с метрикой пространства-времени, а также очевидной малостью эффектов гравитации в микромире 2. Даже в 60-е годы Розенфельд высказывал мнение, что квантовать гравитационное поле бессмысленно, поскольку оно имеет, возможно, чисто классиче-
2 Не так давно появились веские основания думать, что по причинам, «очам не видным», в устройстве микромира гравитации принадлежит важная роль. А полвека тому назад в такую роль можно было только верить. Пророком этой веры был, как известно, Эйнштейн.
139
скую макроскопическую природу [260—261] 3. А ведь Розенфельд был первым, кто рассматривал квантование гравитации на языке формул [259].
Бронштейн в фундаментальности гравитации не сомневался, и для него квантование гравитации, построение полной сGћ-теории — проблема, к которой физика должна обратиться неизбежно. Вместе с тем именно он, как мы увидим, обнаружил настоящую причину, по которой аналогия между гравитацией и электромагнетизмом неточна. . Эта причина не позволяет ожидать многого от попыток по аналогии с квантовой электродинамикой строить квантовую гравидинамику, подставляя гравитон вместо фотона. По Бронштейну, квантовать гравитацию необходимо, но построить полную теорию по образцу электродинамики невозможно. Вместе с тем Бронштейн получил ответы на важнейшие вопросы в области квантовой гравитации, когда cGћ-эффекты слабы и может действовать обычная, «электромагнитная», схема квантования. Эти вопросы касаются соответствия cGћ-теории с cG- и G-теориями гравитации, т. е. взаимоотношения квантовой теории гравитации с ОТО и с ньютоновским законом всемирного тяготения.
5. 2. Корни интереса к сGћ-физике
Итак, настрой физического сообщества не объясняет тему бронштейновской диссертации. Но тогда корни этой темы надо искать в биографии Бронштейна и в биографии самой физики.
а) Квантовая гравитация до Бронштейна.
О том, что необходима квантовая теория гравитации, первым сказал сам Эйнштейн. В 1916 г., всего через несколько месяцев после создания ОТО, при рассмотрении гравитационных волн он отметил: «. . . атом, вследствие внутриатомного движения электронов, должен излучать не только электромагнитную, но и гравитационную энергию, хотя и в ничтожном количестве. Поскольку в природе в действительности ничего подобного не должно быть, то, по-видимому, квантовая теория долж-
3 Статистическую природу гравитации предполагал в 20-е годы и Г. Вейль, надеясь объяснить слабость гравитационного взаимодействия огромностью числа частиц во Вселенной [170].
140
на модифицировать не только максвелловскую электродинамику, но также и новую теорию гравитации» [305, с. 522].
А в 1918 г. в статье о гравитационных волнах Эйнштейн, получив формулу для интенсивности их излучения, сразу же пишет: «Из формулы видно, что интенсивность излучения ни в одном направлении не может стать отрицательной, тем более не может быть отрицательной и полная интенсивность излучения. Уже в прежней работе подчеркивалось, что окончательный результат, согласно которому должна происходить потеря энергии телами вследствие теплового возбуждения, вызывает сомнение во всеобщей справедливости теории. Нам. кажется, что построение усовершенствованной квантовой теории должно повлечь за собой и видоизменение теории тяготения» [307, с. 642]. Эйнштейн, еще не принявший программу единой теории поля, отводил тогда квантовым идеям, как видно, даже более активную роль.
В первом из этих замечаний Эйнштейн имеет в виду проблему электромагнитной нестабильности атома (за несколько лет до этого если не решенную, то преодоленную теорией Бора). Однако его прогноз не мог опираться на количественные оценки. «Высвечивание» атома, рассчитанное в рамках классической электродинамики, приводит к падению электрона па ядро за характерное время
![]()
(в вопиющем противоречии с наблюдениями). А высвечивание энергии атома в форме гравитационного излучения (рассчитанного по формуле Эйнштейна) происходит за характерное время
![]()
Так что ни о каком непосредственном противоречии с эмпирическими данными говорить нельзя. Опирался Эйнштейн, видимо, на аналогию с электромагнетизмом 4.
4 То, что время гравитационного высвечивания τg имеет более чем космологическую величину, дает повод вспомнить, что в те же годы Эйнштейн размышлял над космологической проблемой. То, что для него не важна была величина
141
После того как Эйнштейн в 1916 г. указал на необходимость квантово-гравитационной теории, на ее долю в течение двух десятилетий доставались только отдельные замечания,— физиков занимали другие трудные и более насущные проблемы (квантовая механика, квантовая электродинамика). И эти немногие замечания подразумевали слишком большую аналогию гравитации с электромагнетизмом.
В начале главы уже приводились слова Гейзенберга и Паули 1929 г. из [159] о том, что квантование гравитации не приводит к принципиально новым проблемам по сравнению с электродинамикой. А саму необходимость квантовой гравитации для них обосновывало, помимо указаний Эйнштейна, замечание из статьи О. Клейна 1927 г. [203]. Это замечание сводилось к необходимости единого описания гравитационных и электромагнитных волн, учитывающего постоянную Планка.
Видимо, под воздействием этого же замечания Гейзенберг поставил вопрос, не присущи ли расходимости квантовой электродинамике независимо от «проблемы электрона», т. е. не возникнут ли они и в отсутствие зарядов, если учитывать собственное гравитационное взаимодействие электромагнитных волн. Ответу на этот вопрос посвятил свою статью 1930 г. Розенфельд 5 [259]. Он рассматривал систему, состоящую из электромагнитного и (слабого) гравитационного полей, взаимодействие между которыми определяется линеаризованными уравнениями Эйнштейна и соответственно обобщенными уравнениями Максвелла. В этом приближении (полученном Эйнштейном в 1916 г. ) о геометрической природе гравитации, об искривлении пространства-времени можно забыть, считая, что в
эффекта, связано с тогдашним его представлением о статичности Вселенной. В статической Вселенной, существующей вечно, эффект нестабильности атомов недопустим независимо от его величины. Эту позицию, тогда вполне естественную, любопытно сопоставить с тем, что в наше время возможная нестабильность протона (характеризуемая, кстати, близкой к τg величиной 1032 лет) упоминается в нобелевских лекциях 1979 г. даже как предпочтительная [262]. Так эволюционная космологическая картина подействовала на нормы допустимого в теоретической физике.
5 Благодарность, которую автор выражает Паули «за многочисленные критические замечания и советы», подтверждает связь этой статьи с [159].
142
плоском пространстве-времени имеются два поля — векторное и тензорное. Квантуя эти поля по Гейзенбергу—Паули, Розенфельд подтвердил предположение Гейзенберга о расходимости гравитационной энергии и описал возможные в первом приближении взаимные превращения световых и гравитационных квантов. Однако результаты, полученные Розенфельдом, имели, как подчеркивали Фок и Тамм [173, с. 317, 320], лишь формальный характер, не доходили до существенных физических выводов.
Таким было состояние квантовой гравитации, когда Бронштейн начинал свое исследование этой области. Хотя и Бронштейн в основном рассматривал слабое поле, его работа содержит также анализ, выявляющий принципиальное различие между квантовой электродинамикой и квантовой теорией гравитации без ограничения условием слабости и «негеометричности». Этот анализ показал недостаточность римановой геометрии и обычной схемы квантования поля для полной теории квантовой гравитации. При этом обнаружились границы области существенно квантово-гравитационных явлений.
б) «Отношение физических теорий друг к другу и к космологической проблеме».
Аналогия между электромагнетизмом и гравитацией, возможность распространить методы квантовой электродинамики на новую область была вовсе не главной причиной, из-за которой Бронштейн обратился к квантованию гравитации. Более глубокая причина связана с общей физической картиной мира, о целостности которой Бронштейн начал размышлять рано. Напомним, что уже самые первые его работы касались квантовой и релятивистской физики: статья [1] посвящена квантовой структуре электромагнитного поля, а по статье 1926 г. [4] уже видно знание аппарата ОТО.
Популярную брошюру 1930 г. «Строение атома» Бронштейн закончил характеристикой тогдашнего состояния фундаментальной физики. Упомянув теорию Дирака, квантовую электродинамику, эддингтоновский замысел фундаментальной теории, он не забыл и гравитацию: «Задачей ближайшего будущего является также и установление связи между квантовой механикой и теорией тяготения».
Это предсказание в 1930 г. выглядело вовсе не таким очевидным, как сейчас. Многие физики даже если
143
бы и согласились, что какую-то связь между гравитацией и квантами надо найти, вряд ли включили бы эту задачу в список главных, тем более в книге, посвященной строению атома. Потому что было трудно разглядеть явления, для изучения которых такая связь могла бы пригодиться. С другой стороны, для группы физиков с Эйнштейном во главе, стремящихся к построению единой теории поля, слова «связь гравитации с квантами» означали «выведение квантов из обобщенной теории гравитации». То, что Бронштейн так не думал, видно из энциклопедической статьи [37], раздел которой посвящен единой теории поля. Вывод этого раздела таков: «эйнштейновская программа единой теории поля, вероятно, окажется невыполнимой» и «потребуется какое-то слияние теории относительности с теорией квантов». Для Бронштейна, владевшего обеими теориями, фундаментальны обе, и связь между ними означает именно синтез, а не сведение или подчинение.
Популярная статья [60] (где допустимы более сильные выражения, чем в энциклопедии) кончается словами:
«Будущая физика не удержит того странного и неудовлетворительного деления, которое сделало квантовую теорию "микрофизикой" и подчинило ей атомные явления, а релятивистскую теорию тяготения "макрофизикой", управляющей не отдельными атомами, а лишь макроскопическими телами. Физика не будет делиться на микроскопическую и космическую; она должна стать и станет единой и нераздельной».
В наши дни физика элементарных частиц интенсивно взаимодействует с космологией и подобным высказыванием никого не удивишь. Но что стояло за ним в 1930 г. ?
Прежде всего за ним видны астрономические интересы Бронштейна (космология в то время в гораздо большей степени относилась к астрономии, чем к физике). Однако эти интересы важны не сами по себе.
Для мировосприятия Бронштейна характерно устойчивое внимание не только к физической картине мира, но также и к тому, что можно назвать картой мира физики,— теоретической физики, конечно. Свои представления об этой карте он изложил развернуто в статье 1933 г. «К вопросу о возможной теории мира как целого», в разделе «Отношение физических теорий
144
Схема 1. «Области применимости квантовой механики и специальной теории относительности пересекаются в области классической механики; пунктирным прямоугольником обозначена область применимости еще не построенной "релятивистской теории квант"» [21, с. 22]

друг к другу и к космологической теории». Судя по тому, что материал этого раздела Бронштейн впоследствии воспроизводил еще дважды [50, 81], этой теме он придавал большое значение и был к ней привязан.
Какой же видит карту физической науки Бронштейн? Прежде всего эволюционирующей. Об этой карте он рассказывает, используя все три времени: прошедшее, настоящее и будущее. Как и полагается, на карте существуют границы. Хотя охраняют их не так строго, как государственные, языки по разные стороны каждой границы различаются сильно. Обе структуры в мире теоретической физики — и «пространственная» и «временная» — определяются тремя константами: с, G и ћ. Упомянутые границы — это, конечно, границы применимости фундаментальных теорий, не учитывающих какие-то из универсальных констант с, G или ћ. А эволюция состоит в построении теорий, включающих эти константы органически.
Объяснив предельный характер связей классической механики, квантовой механики, СТО и еще не построенной «релятивистской теории квант», Бронштейн иллюстрирует соотношение этих теорий схемой 1. Затем, после введения константы G в составе ОТО, он чертит новую, расширенную схему 2. По его словам, «в эту схему входят все вопросы, имеющие физический смысл, которые могут быть сформулированы в настоящее время, и возможно даже, что в нее входят все вообще
145
Схема 2. Отношение физических теорий друг к другу и к космологической теории; «сплошные прямоугольники изображают существующие теории в физике, а пунктирные соответствуют еще не решенным проблемам» [21, с. 25]
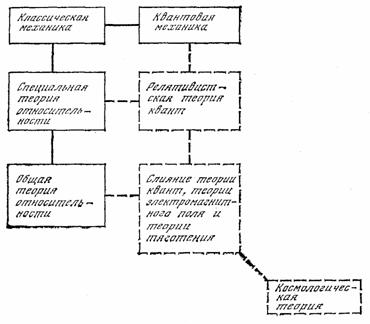
имеющие физический смысл вопросы» [21, с. 25]. Схема показывает, что ближайшая задача — построение релятивистской квантовой теории, сћ-теории. Разъяснив, почему «вопрос о значениях мировых постоянных, имеющих размерность, лишен физического смысла», Бронштейн пишет: «если теория объяснит константы, лишенные размерности, то этим ее задача будет в принципе выполнена, так как лишь от значений этих констант зависит то, почему окружающий нас внешний мир выглядит так-то, а не иначе». Затем приводится пример одной из задач сћ-теории — объяснить безразмерную константу ћс/е2 (постоянную тонкой структуры), что объяснило бы и заряд электрона е посредством постоянных с и ћ. Тогда, впрочем, это было распространенным прогнозом.
Однако в литературе тех времен не найти ничего похожего на продолжение бронштейновского прогноза:
146
«После того как релятивистская теория квант будет построена, задача будет заключаться в том, чтобы построить следующую часть нашей схемы, т. е. слияние квантовой теории (с ее постоянной ћ), специальной теории относительности (с ее постоянной с) и теории тяготения (с ее G) в одно единое целое». (Убедиться в нетривиальности cGћ-схемы Бронштейна можно, сопоставив ее со статьей Паули 1936 г. [250], где ситуация в физике также рассматривается с помощью констант с, G и ћ. )
В качестве примера Бронштейн приводит задачу для сGћ-теории — объяснить безразмерное число ћc/Gme2 = 6∙1044 и тем самым объяснить массу электрона тe через постоянные с, G и ћ.
Но главную задачу для cGћ-теории Бронштейн видит в космологии: «решение космологической проблемы потребует предварительного построения той единой теории электромагнетизма, тяготения и квант, которая обозначена на нашей схеме 2 вторым пунктирным прямоугольником» [21, с. 28]. (Если здесь к электромагнетизму добавить фундаментальные взаимодействия, не известные в 1933 г., то получим высказывание вполне современное. )
Такую cGћ-карту теоретической физики Бронштейн предложил в статье 1933 г. (те же самые идеи он излагал при обсуждении доклада Я. И. Френкеля «О кризисе современной физики» в ЛФТИ 26 февраля 1932 г. [291]).
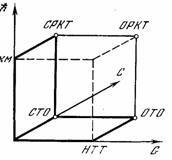
Единственное изменение бронштейновской карты, которое потребовалось в дальнейшем, состояло в переходе от плоского изображения к трехмерному. Внимательно посмотрев на схему 2, можно заметить некоторую ее недостаточность. Например, на этой схеме не поместилась ньютоновская теория гравитации, а также путь от G-теории к cG-теории. Устранить эту асимметрию можно, расположив бронштейновскую схему в трехмерном «пространстве теорий» в cGћ-системе координат (схема 3); это сделал А. Л. Зельманов [186]. В результате получается удобное представление фундаментальной теоретической физики (см., например, [168, гл. 8]).
Была у бронштейновской cGћ-схемы и предыстория. Документальное ее свидетельство — заметка Га-мова, Иваненко и Ландау 1928 г. «Мировые посто-
147
Схема 3. «Пространство» физических теорий в cGћ-системе координат
|
|
НТТ — ньютоновская теория тяготения,
СТО — специальная теория относительности, КМ — квантовая механика, ОТО — общая теория относительности,
СРКТ — специально-релятивистская квантовая теория поля,
ОРКТ — общерелятивистская квантовая теория
янные и предельный переход», опубликованная в ЖРФХО [156].
Заметка начинается с чисто методического, казалось бы, вопроса о построении системы единиц. Авторы отмечают, что можно двумя способами установить единицу измерения для какой-либо новой величины. Можно задать эталон для этой величины произвольно. Либо же, пользуясь каким-то законом, связывающим новую величину с уже известными и содержащим численный коэффициент, можно подобрать эталон так, чтобы этот коэффициент обратился в единицу. В первом случае получается новая мировая постоянная. Во втором — число основных (произвольных) эталонов и число мировых констант остаются неизменными: «мы получаем лишь естественную (по отношению к предыдущим) единицу для измерения нашей величины».
Можно воспользоваться вторым способом и для уменьшения числа основных единиц, положив одну из мировых констант равной единице. Авторы называют это редукцией. По их мнению, «введение новых постоянных и редукция к меньшему числу отобразились в истории физики как смена теорий и их постепенное объединение».
Для полной редукции (т. е. доведения числа эталонов до нуля) необходимо использовать столько независимых мировых констант, сколько основных единиц содержит данная система единиц. Поскольку физических констант много, а наиболее применяема в физике LMT-система размерностей, то возникает вопрос, какие три из всех констант следует выбрать. Авторы
148
предлагают руководствоваться «двумя эвристическими положениями»: степенью общности теории, которую представляет данная константа, и пробой постоянной на предельный переход в цепочке «классическая теория — "вульгарная" [полуклассическая] теория — законченная теория».
В результате авторы за «истинные» постоянные принимают ћ, с-1, G и отмечают, что так, следуя Планку, можно перейти к физике без размерностей, получив «естественные» единицы для всех физических величин 6.
Такое рассмотрение приводит авторов к единственному практическому выводу, касающемуся, правда, важной для того времени проблемы: «не имея еще теории электрона, можно, однако, на основании теории размерностей вывести некоторое заключение о характере этой теории»; так как [е] = ([ћ] [с])1/2, [m] = =([ћ] [c] / [G]) 1/2, «обречены на неудачу часто производимые попытки построить теорию неквантового электрона в общей теории относительности»: если ћ=0, с≠∞, G≠0, то е=0 и т=0. Мишень здесь, конечно, сам Эйнштейн и другие приверженцы единой теории поля, которые надеялись получить ћ-эффекты из cG-теории, более общей, чем ОТО.
Для тех, кто имеет представление об авторах этой заметки, она выглядит очень странно. Бросается в глаза явная «нерезультативность» этой публикации в научном журнале (ни одной производной, ни одного интеграла!). Если еще учесть утроенный авторский потенциал (это, кстати, единственная их совместная работа) и молодость авторов, то недоумение только возрастает. Трудно удержаться от предположения, что Ландау должен был назвать такую заметку «филологией» (самая мягкая из его отрицательных оценок). Ни у кого из троих в других работах не видно следов этой заметки.
6 Упоминание Планка привязывает этот текст сразу и к прошлому, и к будущему. В 1899 г. Планк ввел — с чисто метрологической целью — естественные единицы на основе констант с, G и только что появившейся ћ; а, как впервые обнаружилось в диссертации Бронштейна 1935 г., эти же самые планковские величины соответствуют квантовым границам ОТО (см. разд. 5. 4).
149
Только Гамов, более других соавторов склонный к научно-популярному жанру, обсуждал в своих книгах константы с, G, ћ. Он даже дал инициалы С. G. Н. своему герою мистеру Томпкинсу, банковскому клерку, заставив его интересоваться физикой [149]. Но то, как Гамов обращался с этими константами, скорее доказывает, что заметка 1928 г. (в которой с, G, ћ одинаково выделены) не оставила в нем глубокого следа. Он сомневался в фундаментальности G, то подозревая, что это замаскированный квадрат константы слабого взаимодействия, то легко допуская переменность G, то вообще исключая ее из числа «истинных констант» [153, с. 157]. И даже когда Гамов писал обо всех трех константах, он делал это через запятую, рассказывая в отдельности о с-, G- и ћ-теориях, но не о cGћ-физике. Мало того, что он в угоду своей выдумке с инициалами изменил буквы с и ћ со строчных на прописные; он еще и без всяких колебаний — в педагогических целях — менял сами величины с, G, ћ, считая, что это помогает понять физику [149].
Такое вольное обращение с фундаментальными константами, но мнению Бора, было скорее глупым, чем смешным [241, с. 189]. Вряд ли этот педагогический прием нашел бы сочувствие и у Эйнштейна. Оба великих физика считали значения универсальных констант настолько существенными для устройства мироздания, что их нельзя менять без изменений или даже разрушения самого этого устройства [310, т. 4, с. 281] (речь, разумеется, идет об изменениях безразмерных комбинаций констант; остальные просто фиктивны). Так же относился к фундаментальным константам и М. П. Бронштейн.
Как мы видим, даже в Гамове, с его «филологическими» наклонностями, не узнать автора cGћ-заметки 1928 г.
Вероятно, читатель уже догадался, к чему его склоняют. Действительно, и ознакомившись с последовательными и настойчивыми сGћ-построениями Бронштейна, трудно допустить его непричастность к заметке 1928 г. Можно, конечно, предположить, что идею, к которой ее авторы были довольно равнодушны, Бронштейн принял близко к сердцу, а затем ее развил, «геометризовав» в виде своей cGћ-схемы. Но если помнить об устойчивом интересе Бронштейна к соотношениям теорий, о ключевых для него словах «гра-
150
ницы применимости теории» (появившихся уже в первой его работе 1925 г. ), то легче предположить другое.
В 1927 г. (заметка датирована 20. 10. 1927 г. ) три мушкетера — Джо, Димус и Дау только что расстались с университетом, Аббат еще на положении студента. Джаз-банд в расцвете. И преданность его участников науке нисколько не препятствовала веселью и озорству. Озорным было и рождение заметки, в которую мы так пристально вглядываемся. По свидетельству А. И. Ансельма, она сочинялась во время не очень сытного, но веселого КУБУЧевского обеда в «Астории». И сочинялась ко дню рождения прекрасной дамы — И. Сокольской, также участницы Джаз-банда. При публикации посвящение исчезло. Однако и без него ясно, что заметка трех авторов не соответствовала их собственным стандартам научной работы. Хотя для физических разговоров тема была пригодна. Из устного арсенала ее, видимо, извлекли, когда возникла срочная надобность написать статью 7. А в арсенал этот, где идеи очень быстро коллективизируются, она могла попасть как раз благодаря Бронштейну (который 20 октября 1927 г. обедал, возможно, не в компании своих друзей-физиков, а в обществе астрономов или филологов).
В пользу этого предположения говорит еще то, что Бронштейн, очень аккуратный в ссылках, заметку своих друзей нигде не упоминает 8.
в) У истоков квантово-релятивистской астрофизики.
Герой нашей книги ожидал сGћ-теорию, питаясь не только общими соображениями, воплощенными в сСћ-схеме. Иначе он был бы только философствующим физиком. Но он был физиком практикующим. И зачатки cGћ-физики находил среди конкретных физико-математических выкладок. Такие выкладки со-
7 Было еще одно назначение этой заметки. Ее авторы не восторгались средним уровнем статей ЖРФХО (главным редактором которого был А. Ф. Иоффе) и считали, что там печатается «все что попало». Продемонстрировать это они решили «филологической» статьей. На обложке «Physikalische Dummheiten», в редколлегию которого входили авторы, красовалось соотношение: ЖРФХО = lim «Phys. Dumm. ».
ћ→0, c→∞
8 В статье [21], ссылаясь на работу Ландау и Пайерлса, Бронштейн благодарит Ландау за то, что «целый ряд идей, легших в основание настоящей статьи, почерпнул из бесед сним».
151
держатся в его работах о релятивистском обобщении принципа неопределенности (см. разд. 5. 4), о свойствах излучения при очень высоких — астрофизических — температурах, о внутреннем строении звезд.
Большую статью Бронштейна 1933 г. [20] относят к основополагающим для теории белых карликов [198, с. 110]. В ней действительно физически очень ясно и внимательно рассмотрено равновесие гравитирующего шара, состоящего из вырожденного ферми-газа в не- и ультрарелятивистском предельных случаях 9. В этой работе также впервые получено уравнение для такой звезды в общем случае, когда степень релятивизма меняется от центра звезды к поверхности [20, с. 99]. Бронштейн отметил, однако, что решение этого уравнения связано с «утомительными вычислениями». Вычисления проделал в 1935 г. Чандрасекар [296]. Теорию белых карликов он довел до количественных результатов, полученных численным интегрированием (Чандрасекар отметил, что само уравнение он дал в предварительной заметке 1934 г. [295], однако советские астрофизики знали, что Бронштейн получил его первым [92—93]).
И все же статья Бронштейна, как и предшествующая ей заметка Ландау [214] (на которую он ссылается), были посвящены не белым карликам; в обеих статьях белые карлики не упоминаются. Уже названия статей говорят о том, что авторы видели перед собой более общую проблему — проблему физической природы звезд и механизма их излучения. Авторов-физиков звезда интересовала прежде всего как загадочный физический объект. Это, в частности, объясняет, почему Бронштейн не «пробивал» решение полученного им уравнения (для «чистого» астрофизика задача несомненно достойная).
Статью [20] Бронштейн начинает с критики теории Эддингтона за то, что она пыталась описать устройство звезды независимо от вопроса об источнике звездной энергии. Затем, следуя Ландау, он рассматривает газовый шар без всяких источников энергии при нулевой температуре. Такая звезда из классиче-
9 В 1926 г. Р. Фаулер объяснил большую плотность белых карликов тем, что они состоят из вырожденного ферми-газа; релятивистский ферми-газ в применении к теории сверхплотных звезд впервые рассматривал в 1928 г. Я. И. Френкель [290-291].
152
ского идеального газа не может быть в равновесии и будет сжиматься, пока не начнут проявляться законы квантовой статистики. Именно так предметом рассмотрения и стало равновесие шара из вырожденного ферми-газа. Следует отметить, что результатом заметки Ландау тогда считалось вовсе не существование предельной массы для такой конфигурации
![]()
Этот замечательный результат, как указывает Бронштейн, впервые получен Стонером в 1930 г. [266]. Однако Стонер не увидел ничего страшного в неограниченном сжатии звезды с массой больше предельной: он считал, что такое сжатие будет приводить просто к разогреву и излучению.
Ландау же, поскольку при массе, большей М0, «во всей квантовой теории не существует причины, которая предотвратила бы сжатие системы в точку», а с другой стороны, «в действительности такие массы мирно существуют в виде звезд», приходит к заключению, что «все звезды тяжелее, чем 1,5 М0, содержат область, в которой нарушаются законы квантовой механики (и тем самым квантовой статистики)»; «можно с большой вероятностью предположить, что такую патологическую область имеют все звезды» и что «именно наличие таких областей и делает звезды звездами». «Следуя красивой идее проф. Нильса Бора», Ландау предлагает объяснить излучение звезд «просто» несохранением энергии в релятивистской квантовой механике: эта теория должна действовать в патологической области, когда атомные ядра придут в тесный контакт и образуется одно гигантское ядро 10.
Таким образом, самого Ландау астрофизика приводила только к проблеме cћ-теории, G играла роль внешнего фактора, так сказать, стенок сосуда. А для Бронштейна, вполне принимавшего выводы Ландау, астрофизический материал говорил о необходимости построения cGћ-теории: «Релятивистская теория квант,
10 Сейчас нелегко понять отношение Ландау к менее «патологическим» источникам звездной энергии, в частности к термоядерному синтезу водорода в гелий: «Было бы очень странно, если бы высокие температуры могли помочь делу уже только потому, что помогают кое-чему в химии (цепные реакции!)». Но, желая понять физику того времени, необходимо понять и этот скепсис (см. гл. 4).
153
соединяющая волновую механику со специальным принципом относительности, должна будет подвергнуться дополнительному расширению в духе общего принципа относительности» [20, с. 102]. Такую необходимость Бронштейн поясняет простым соображением: если Солнце сожмется до ядерной плотности, то его радиус станет сравним с гравитационным.
А одним из наиболее интересных следствий указанных соображений Бронштейн назвал необходимость создания новой физической теории, применимой ко всем частям Вселенной, при этом «сами понятия пространства и времени, а следовательно и формулировка общего принципа относительности и уравнений тяготения, должны подвергнуться в этой будущей теории каким-то весьма глубоким преобразованиям» [20, с. 103]. Эти рассуждения, стоявшие за cGћ-схемой [21], были конкретизированы в диссертации.
5. 3. Квантовая теория слабого гравитационного поля
Результаты своей работы по квантованию гравитации Бронштейн изложил в двух статьях: краткий вариант на немецком языке — «Квантовая теория слабых гравитационных полей» — датирован августом 1935 г., подробный — «Квантование гравитационных волн» — 14 декабря 1935 г.
Большая статья (42 ЖЭТФовские страницы) совпадает с диссертацией по названию и, видимо, также и по тексту в целом. Работа состоит из трех частей. Первая, посвященная гравитационным волнам в классическом случае, служит введением для следующих двух, в которых развивается квантовая теория слабого гравитационного поля в пустоте и при наличии материи.
Исходя из данной Гейзенбергом и Паули общей схемы квантования полей, Бронштейн рассмотрел гравитацию в приближении слабого поля, когда можно не учитывать геометрический характер гравитационного поля и рассматривать его как тензорное поле в плоском пространстве-времени.
Намерение насытить диссертацию длинными формулами, о котором М. П. поведал И. К. Кикоину, осуществить было нетрудно. Работа содержит весьма громоздкие математические выкладки (при этом еще про-
154
межуточные этапы опущены). В этом обстоятельстве вполне отразилась специфика рассматриваемой проблемы.
Все дело в том, что приближение слабого поля в ОТО имеет и специальный, и в то же время достаточно общий характер — число степеней свободы максимально возможное, и десятикомпонентность гравитационного «потенциала» не укрощается ни симметриями, ни мощью римановой геометрии, потому что общая ковариантность в этом случае фактически уже не действует. Однако координатный произвол достаточно велик, и необходимо изрядно потрудиться, чтобы отделить координатные эффекты от физических.
Мы не станем вникать в техническую сторону бронштейновского квантования слабой гравитации, а отметим только некоторые характерные особенности его работы.
В классической части гравитационные волны описываются посредством четырехзначкового тензора Римана—Кристоффеля (а не посредством малой добавки к метрике Минковского, как обычно делают), что дает возможность сразу же исключить фиктивные — координатные — гравитационные волны. Со всей отчетливостью выявляется калибровочная свобода системы (Бронштейн пользуется терминами «Eichungtransforma-tion» и «Eichung») и тот факт, что гравитационная волна имеет две степени свободы.
В квантовой части получены два очень существенных результата. Рассчитана интенсивность излучения энергии, происходящего при испускании гравитационных квантов материальной системой, и показано, что в классическом пределе (ћ→0) квантовая теория гравитации дает такие же результаты, как классическая: квантовая формула Бронштейна переходит в классическую квадрупольную формулу Эйнштейна.
Затем к гравитации применена идея, которую по отношению к электродинамике высказал Дирак и развили Фок и Подольский в 1932 г. [281], получившие из квантовой электродинамики кулоновскую силу. Аналогично этому Бронштейн получил ньютоновский закон тяготения как следствие квантово-гравитационного закона взаимодействия. При этом он обращает внимание на то, что, несмотря на сходство кулоновского и ньютоновского выражений для взаимодействия поля с частицей, противоположные знаки этих сил следуют
155
вполне естественно из общего квантово-механического формализма 11.
Оба результата, которые Бронштейн получил из рассмотрения квантованного слабого гравитационного поля,— это, казалось бы, всего лишь естественные требования принципа соответствия, и они могли только, самое большее, свидетельствовать о правильности способа квантования. Однако в действительности эти результаты имели принципиальное значение, поскольку особое положение гравитационного поля, отождествление его с геометрией пространства-времени вызывало, как уже говорилось, сомнения в необходимости синтеза квантовой теории и ОТО. Мнение о слишком особом характере гравитации, отделяющем ее пропастью от других физических полей, было довольно распространенным. Не менее известной была тогдашняя позиция Эйнштейна, считавшего, что от истинной, полной физической теории общую теорию относительности отделяет, если можно так выразиться, гораздо меньшее расстояние, чем квантовую теорию.
Исследование Бронштейна продемонстрировало глубокие связи классического и квантового (хотя и неполного) описаний гравитации и тем самым свидетельствовало о возможности и необходимости квантового обобщения ОТО.
Заметим, что термином «гравитон» Бронштейн не пользовался, хотя само это слово уже существовало. В типографском исполнении оно имеется в статье Бло-хинцева и Гальперина 1934 г. в журнале «Под знаменем марксизма» [111], и, судя по тексту, нет оснований думать, что термин родился здесь; видимо, он существовал уже по меньшей мере в устном виде. Эта статья, упоминавшаяся в главе 4, имела совсем не гравитационное название «Гипотеза нейтрино и закон сохранения энергии» и была написана, когда теория бета-распада, построенная Ферми на основе гипотезы нейтрино, пользовалась уже широким признанием. Однако последний раздел этой статьи «Природа нейтри-
11 Результат отнюдь не был простым переписыванием формул Фока, и тот, рассказывая в газете «Техника» (18. 3. 1936 г. ) о своей с Дираком и Подольским работе, отметил: «Идеи, лежащие в основе этой теории, были с успехом применены ленинградским физиком М. П. Бронштейном к тяготению, причем ньютоновский закон притяжения был выведен им из представления о "квантах тяготения"».
156
но» содержит соображения, очень любопытные для cGћ-истории, и мы их приведем полностью, несмотря на большой объем цитаты.
«Взаимодействие заряженных частиц (закон Кулона) с современной точки зрения [ссылка на статью Дирака 1932 г. ] рассматривается динамически, а именно как результат непрерывного испускания и поглощения квантов света взаимодействующими частицами. (. . . )
Весьма интересно сравнение свойств нейтрино и так называемого гравитона. До сих пор известные в физике поля распадаются на два класса: электромагнитные и гравитационные. (. . . )
Все многочисленные попытки, в первую очередь самого Эйнштейна, найти связь между электромагнитными явлениями и явлениями гравитационными, начиная с попытки гениального М. Фарадея, кончались неудачей и заводили в дебри формализма. (. . . )
Но излучение электронных [электромагнитных?] волн не единственная причина нестабильности атома. Благодаря излучению гравитационных волн движущимся электроном атома, аналогичным планете в Солнечной системе, атом также будет терять энергию. Поэтому, чтобы понять стабильность атомов, нужно предположить, что не только электромагнитная энергия, но и энергия гравитационная излучаются не в виде волн, но квантами энергии: в первом случае — квантами электромагнитной энергии — квантами света (фотонами), во втором случае — квантами энергии тяготения — «гравитонами». Гравитоны, однако, не имели никакого значения в современной квантовой теории атома ввиду того, что вероятность их излучения, как можно посчитать, ничтожно мала в сравнении с вероятностью излучения светового кванта. Равным образом малы и гравитационные взаимодействия по сравнению с взаимодействиями электромагнитными. Излучение и поглощение гравитонов должны были бы вести к взаимодействию частиц по закону Ньютона (к гравитационному полю), подобно тому, как поглощение и излучение квант света заряженными частицами ведет к закону Кулона. Эти гравитоны должны, подобно квантам света, обладать массой только в состоянии движения со скоростью света. Они, разумеется, не несут электрического заряда. С этой точки зрения они крайне схожи с введенными Ферми нейтрино. Тот факт, что вероятность излучения гравитона крайне мала по сравнению с вероятностью излучения фотона, имеет значение только для заряженных частиц. Незаряженная частица, какой является нейтрон, вообще не может излучать квант света, и из-
157
лучение гравитонов может для него иметь существенное значение. Бета-распад как раз является таким процессом, в котором мы и имеем дело с квантовым переходом нейтрона. Приведенное выше сравнение свойств гравитона со свойствами нейтрино, обнаруживающее их сходство, может быть, свидетельствует о том, что, вообще говоря, маловероятный процесс излучения гравитонов становится практически наблюдаемым при бета-распаде. Если бы нейтрино действительно были гравитонами, это означало бы, что современная физика подошла к ликвидации все еще существующей непроходимой грани между гравитацией и электромагнетизмом.
Тем не менее все же трудно, по теоретическим соображениям, отождествить гравитоны с нейтрино, так как трудно допустить, что гравитоны имеют спин, равный ½, каким обладает нейтрино. В этом отношении гравитон более схож с квантом света, нежели с нейтрино. Но нельзя не [?] считать, что возможность их отождествления совершенно исключена теорией. Пока все же более правильно рассматривать нейтрино как самостоятельный сорт частиц».
Приведенный текст производит довольно странное впечатление. С одной стороны, многое в нем похоже на предвосхищение результатов Бронштейна. С другой, помимо неточностей и некоторой легковесности, в глаза бросается «несамосогласованность» текста, как будто его авторы имеют свое мнение, но не согласны с ним.
Для приоритетных подозрений оснований, однако, мало в силу следующих обстоятельств. Статья в журнале «Под знаменем марксизма» имела популяризаторский и методологический характер, и ее авторам явно интереснее описывать научную ситуацию, чем пунктуально расставлять ссылки; в частности, уже знакомое нам замечание Эйнштейна 1916 г. пересказано анонимно. Совершенно незаметны какие-либо cGћ-интересы авторов в те годы; Д. И. Блохинцев занимался тогда физикой твердого тела, а не квантовой теорией поля или гравитацией [109]. Блохинцев был учеником и сотрудником И. Е. Тамма — одного из оппонентов бронштейновской диссертации; и трудно представить, чтобы Тамм умолчал о предшествующих идеях, если бы они действительно принадлежали его ученику, а не Бронштейну. Дополнительное свидетельство того, что квантово-гравитационные идеи не были родными для Блохинцева и Гальперина,— полное отсутствие каких-
158
либо упоминаний о гравитации в их статье 1936 г. «Атомистика в современной физике» [112], хотя поводов сказать о квантах гравитации в ней более чем достаточно (и когда Блохинцев вернулся — в 50-е годы — к вопросу о связи гравитации с физикой элементарных частиц, его отношение к такой связи было весьма скептическим). По всем этим причинам легче предположить, что в статье Блохинцева и Гальперина 1934 г. излагаются какие-то устные дискуссии с участием Бронштейна. А если так, то, значит, его диссертационная работа, выполненная летом 1935 г., была завершением и оформлением более ранних идей.
Идея о связи гравитации и нейтрино, о которой говорится в статье Блохинцева и Гальперина, была не так уж экзотична. По свидетельству Гамова, «Нильс Бор еще в 1933 г. задавал вопрос: в чем разница между нейтрино и квантами гравитационных волн?», и сам Гамов считал «связь между нейтрино и гравитацией волнующей теоретической возможностью» [152, с. 143] 12.
Отзвук того же вопроса Бора можно усмотреть и в книге его ученика Дж. Уилера «Гравитация, нейтрино и Вселенная» [273].
Идея о родстве нейтрино и гравитации не вызывала никакого сочувствия у Бронштейна [41],— для такого родства тогда не было никаких глубоких причин. Во всяком случае их не видно в cGћ-системе отсчета, в которой Бронштейн рассматривал фундаментальные теории физики. Нет таких причин и сейчас; нет оснований говорить, что гравитация находится в большем родстве со слабым взаимодействием, чем с электромагнитным.
12 О возможности такой связи Гамов впервые написал в 1937 г., пытаясь выжать все из идеи обменных парных сил. Поскольку взаимодействие, обусловленное обменом пар еν, оказалось в 1012 раз слабее, чем надо для объяснения ядра, Гамов предположил, что за ядерные силы отвечает обмен парами е+е–, т. е. что обменное ее-взаимодействие в 1012 раз сильнее eν-взаимодействия. Отсюда следовало предположение, что существует и обменное νν-взаимодействие и что оно еще в 1012 слабее eν-взаимодействия. Поэтому излучение пар нейтрино «ассоциировалось» с испусканием квантов гравитационного излучения [150]. И даже в 1962 г. Гамов писал [152], что «пара нейтрино могла бы дать спин 2» (т. е. гравитон). Таким образом, объяснение гравитации было побочным результатом, а электромагнетизм и геометрическая природа гравитации оставались совершенно в стороне. Такое изобретательство было чуждо Бронштейну.
159
Только в пунктирном сGћ-прямоуголънике на бронштейновской схеме было место для нейтрино. Таково же мнение на этот счет и современной физики, ожидающей Великого объединения взаимодействий.
А что касается бронштейновских результатов по квантовой теории слабого гравитационного поля, то их значение не зависит от судьбы единой теории. На защите диссертации Фок сказал: «В рассмотренном М. П. приближении сомневаться нельзя. Если даже будет неверной теория Эйнштейна, то результаты М. П. не изменятся» [173, с. 319] (корявость слога здесь можно отнести на счет стенографии; Фок, видимо, говорил о квантовой ограниченности ОТО). Действительно, результаты Бронштейна сохраняют свое значение и сейчас, поскольку навсегда сохранит свое значение вопрос соотношения фундаментальных теорий гравитации и областей их применимости.
На определенных этапах развития физики возникает потребность в обобщении данной фундаментальной теории. Гравитация в XVII в. получила G-теорию, в 1915 г. — cG-теорию, а сейчас все еще ожидает полную, последовательную cGћ-теорию. Но слово «обобщение» в теоретической физике имеет специфический смысл. Развитие теории включает в себя и обобщение и специализацию, возрастающую гибкость (общность) отдельных компонентов теории и возрастающую жесткость (однозначность) конструкции теории в целом. Обобщение происходит по отношению к количественным предсказаниям в конкретных задачах, а по отношению к структуре теории принцип соответствия действует непросто. Теоретическая физика — это иерархия моделей, относящихся друг к другу более сложно, чем частный случай к общему; соотношение фундаментальных теорий имеет предельный характер (как в случае G-, cG- и cGћ-теорий гравитации). При этом «устаревшие» модели, как правило, не утрачивают практического значения и остаются в арсенале физики.
Поэтому результаты Бронштейна, относящиеся к приближению слабой квантовой гравитации, сохранят свой смысл и значение и в будущем. Не следует думать, что такая оценка лишь проявление сверхбережного отношения историка к правильным физическим результатам. Например, с тех пор как была построена квантовая теория слабой гравитации, проделано большое количество расчетов в рамках, так сказать, квантовой
160
гравидинамики: рассчитывались разнообразные реакции элементарных частиц с участием гравитонов. Но правильность подобных — сложных математически — расчетов отнюдь не делает их физически осмысленными (даже если не говорить о неперенормируемости линейной квантовой гравидинамики). Дело в том, что результат любого подобного расчета должен содержать безразмерный множитель типа 10–40 и не может иметь ощутимую величину в условиях применимости самой теории. Ощутимыми и даже принципиально важными квантово-гравитационные эффекты могли бы стать при больших концентрациях энергии (которые бы скомпенсировали число 10–40), т. е. в астрофизических и космологических условиях, однако в таких условиях уже неприменима сама линейная квантовая гравидинамика. Слабость гравитационного взаимодействия могла бы еще компенсироваться достаточно большим — космологическим — временем взаимодействия; такую ситуацию Бронштейн рассмотрел год спустя (см. разд. 5. 5).
5. 4. «. . . Принципиальное различие между квантовой электродинамикой и квантовой теорией гравитационного поля». Квантово-гравитационные границы
Рассказ предыдущего раздела о квантово-гравитационных результатах Бронштейна в некоторой мере искажает историко-научную ситуацию, потому что там рассказано лишь о решении задач, относящихся к переходам «сверху вниз» — символически: (cGћ)→(cG) и (cGћ)→(G). А этим задачам в работе Бронштейна предшествует анализ измеримости гравитационного поля, касающийся переходов «снизу вверх»: (cG)→ →(cGћ) и (сћ)→(сGћ). Этот анализ, приведший к обнаружению квантово-гравитационных границ, особенно интересен для сегодняшней теоретической физики.
а) Проблема cћ-измеримости.
То что Бронштейн, занявшись квантованием гравитации, уделил внимание вопросу измеримости, вполне естественно и для биографии науки, и для научной биографии Бронштейна. История этого вопроса начинается с принципа неопределенности (1927), который установил ћ-ограничения на применимость понятий, оставшихся от классической физики. Соотношения неопределенностей ограничивали только совместную измеримость некоторых —
161
сопряженных — пар величин, например координаты и импульса
![]()
но оставалась возможность говорить о сколь угодно точном значении каждой величины в отдельности.
Сразу после того, как был осознан смысл ћ-ограни-чений, возник вопрос о характере квантовых ограничений при учете релятивизма — о сћ-ограничениях. Мысленные эксперименты (начиная с гейзенберговского микроскопа) давали сколь угодно точные результаты, лишь игнорируя с-теорию. И, кроме того, важнейший физический объект — электромагнитное поле — был релятивистским, как известно, еще до создания теории относительности; ведь уравнения Максвелла включают в себя константу с. Ограничения измеримости, или соотношения неопределенностей, для электромагнитного поля рассматривали сам Гейзенберг [158, с. 41], Фок и Йордан [280].
Однако особенно большое внимание привлекло к себе исследование сћ-ограничений, выполненное Ландау и Пайерлсом в 1931 г. Анализ мысленных экспериментов в сћ-области приводил уже не только к парным, но и к индивидуальным неопределенностям величин, описывающих частицу и поле. Согласно Ландау и Пайерлсу понятие «поле в точке» полностью неопределимо. На этом основании они ставили под вопрос тогдашнюю квантовую теорию электромагнитного поля и предсказывали, что «в правильной релятивистской квантовой теории, которая пока не существует, не будет ни физических величин, ни измерений в смысле волновой механики» [221, с. 69].
Этот прогноз вполне соответствовал другим вопиющим указаниям на принципиальную недостаточность тогдашней физики (±-трудность уравнения Дирака, парадокс Клейна, расходимость собственной энергии и др. ) В начале 30-х годов в неизбежной сћ-перестройке понятий (включая понятие пространства-времени) были уверены многие теоретики, и анализ измеримости поля был наиболее фундаментальным доводом.
Ландау и Пайерлс считали свою работу развитием идей Бора и теоретическим обоснованием его гипотезы о несохранении энергии. Однако сам Бор столь решительный вывод не принял, и в 1933 г. «обезвредил» его (совместно с Розенфельдом) после упорных дискуссий
162
с Ландау и Пайерлсом. Слабое место в их рассуждениях Бор усмотрел в том, что они для измерения поля использовали в качестве пробных тел только точечные заряды — идеализацию, перенесенную в теорию поля из теории атома. Однако «для проверки аппарата квантовой электродинамики,— подчеркнул Бор,— допустимы лишь измерения с пробными телами конечных размеров, внутри которых распределен заряд; это следует из того, что всякое однозначным образом вытекающее из этого аппарата утверждение относится к средним значениям компонент поля, взятым по конечным областям пространства-времени» [121, с. 128]. Это положение Бор связывал с тем, что аппарат квантовой электродинамики не включает в себя органически каких-либо предположений об атомизме электричества. А если в мысленных измерениях пользоваться полным произволом в отношении заряда пробного тела, то указанные Ландау и Пайерлсом пределы действительно снимаются.
Характер сћ-теории занимал Бронштейна с тех пор, как ее «призрак начал бродить» по физике. И соображения, связанные с наблюдаемостью, с измеримостью физических величин играли значительную роль. В 1931 г. в рецензии на книгу Дирака, упрекая того в недооценке квантово-релятивистских проблем, Бронштейн цитирует ехидное определение Паули, прозвучавшее, видимо, на Одесском съезде 1930 г. : «Die Observable ist eine Grösse, die man nicht messen kann» («Наблюдаемая — это величина, которую невозможно измерить»); в формулировке Бронштейна: «принцип неопределенности обычной квантовой механики чересчур определен для релятивистской теории квантов».
На работу Бора—Розенфельда Бронштейн откликнулся заметкой, посвященной измеримости в сћ-области [24]. Надо сказать, что весьма объемную статью Бора—Розенфельда не назовешь очень ясной. Заметка Бронштейна раз в 20 короче. И ее выкладки лучше соответствуют ориентировочному характеру мысленных экспериментов, чем хитроумные рассуждения [121], в которых вместе с мысленными пружинками и массивными каркасами участвуют произвольно большие заряды в произвольно малых объемах (природе не известные).
При этом Бронштейн в ясной форме воспроизвел боровский вывод о несмертельном характере сћ-ограничений для теории поля.
163
Проведем упрощенные выкладки, измеряя напряженность электромагнитного поля Е по изменению импульса пробного тела с зарядом Q и массой М:
![]()
Неопределенность ΔE составляют два слагаемых. Первое порождается неопределенностью измерения импульса:
![]()
Второе слагаемое — это «обратное» поле, источником которого является ток — произведение заряда пробного тела на его скорость. Неопределенность этой скорости (скорости отдачи), соответствующая локализации пробного тела с неопределенностью Δx, равна
![]()
и «обратное» поле
![]()
Вводя плотности заряда и массы пробного тела ρ=Q/Δx3, μ=М/Δx3 (объем тела V~Δx3) и учитывая, что Δp~ћ/Δx, получим
![]()
Устремляя Δx к нулю и полагая, что ρ и μ достаточно быстро, но по разным законам стремятся к бесконечности, можно считать, что ΔE→0 при Δx→0. Тем самым оправдывается понятие «электромагнитное поле в точке».
Бор особенно подчеркивал, что неопределенность поля, обусловленная влиянием самого пробного заряда, может быть сделана, вопреки Ландау—Пайерлсу, сколь угодно малой, а Бронштейн указал, что для максимальной точности измерения поля не следует стремиться к наименьшей реакции излучения на пробное тело. И хотя общий вывод остался прежним, Бронштейн подчеркнул, что возможности теории когда-нибудь придется согласовать с возможностями природы: «Принципиальная невозможность измерить с произвольной точностью поле в будущей релятивистской теории
164
квант будет связана с принципиальным атомизмом материи, т. е. с принципиальной невозможностью беспредельно увеличивать [плотность заряда] ρ».
Таким образом, в заметке 1934 г. Бронштейн сбалансированно представил сћ-ограничения на измеримость электромагнитного поля. Поэтому не удивительно, что год спустя он обратился к анализу измеримости гравитационного поля.
b) cGћ-измеримость и квантовые границы ОТО. Проследим за этим анализом внимательно, вместе с Бронштейном «немного мысленно поэкспериментируем!» (так называется параграф в [30]). Напомним сначала, что в приближении слабого гравитационного поля метрический тензор gik представляется в виде
![]()
где δik — плоская метрика Минковского, а все величины hik<<1. В этом случае, как показал еще Эйнштейн в 1916 г., общие нелинейные уравнения ОТО сводятся к линейным (с точностью до членов высшего порядка малости по hik):
![]()
(1)
где Tik— тензор энергии-импульса, а κ=16πG/с2.
Сконструировав подходящий для этого случая гамильтониан гравитационного поля, Бронштейн выписывает перестановочные соотношения в соответствии с общей схемой квантования полей Гейзенберга и Паули 1929 г.
Однако, прежде чем перейти к построению квантовой картины слабого гравитационного поля, Бронштейн обращается к вопросу, касающемуся синтеза квантовых и гравитационных представлений в общем случае, а не только в случае слабого поля. После краткого обсуждения перестановочных соотношений он пишет:
«Можно было бы думать, что здесь, как и в квантовой электродинамике, получается вполне последовательная квантово-механическая схема, содержащая величины, которые, правда, не всегда могут быть измеряемы с произвольно задаваемой точностью одновременно, но каждая из них может быть сколь угодно точно измерена в отдельности. . . . Чтобы понять природу тех физических условий, которые могут сделать это утверждение недействительным, рассмотрим в качестве простейшего примера измерение величины [00, 1], т. е.
165
одной из скобок Кристоффеля [играющих, как известно, роль напряженности гравитационного поля]. Эта величина может быть измерена посредством пробного тела, движущегося со скоростью, бесконечно малой по сравнению со скоростью света» [31, с. 214]. В этом приближении, если считать и гравитационное поле слабым, уравнение геодезической для координаты х1
![]()
переходит в уравнение
![]() (2)
(2)
здесь и далее х≡х1, Г1,00 — современное обозначение символа Кристоффеля [00,1].
Для измерения значения Г1,00, среднего по объему V и за промежуток времени Т (а согласно Бору—Розенфельду в квантовой теории поля следует говорить только о такого рода измерениях), надо измерить компоненту рх импульса пробного тела, имеющего объем V, в начале и в конце промежутка времени Т, поскольку в рассматриваемом приближении
![]()
где ρ — плотность пробного тела. Поэтому если измерение импульса имеет неопределенность Δрх, то неопределенность
![]() (3)
(3)
Неопределенность импульса рх состоит из двух слагаемых: обычного квантово-механического
(Δрx)1=ћ/Δx
(где Δx — неопределенность в координате) и «члена, связанного с полем тяготения, создаваемого самим измерительным прибором вследствие отдачи при измерении импульса». Второе слагаемое Бронштейн оценивает следующим образом. Уравнение (1) с учетом используемого приближения дает
![]()
Если на отдельное измерение импульса затрачивается время Δt (при этом должно быть Δt<<T), то неопреде-
166
ленность величины h01, связанная с неопределенностью скорости отдачи vx~Δx/Δt, имеет порядок
![]()
и согласно (2) неопределенность напряженности гравитационного поля
![]()
Соответствующая неопределенность импульса, связанная с собственным гравитационным полем пробного тела, имеет тогда порядок
![]()
Таким образом, общая неопределенность импульса
![]()
(4)
Чтобы сделать эту неопределенность минимальной, нужно, как следует из (4), выбрать
![]()
Тогда
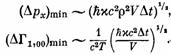 (5) (6)
(5) (6)
Продолжительность измерения импульса Δt ограничивается снизу двумя условиями. Во-первых, должно быть Δt>Δx/c, чтобы скорость отдачи, вызванной изменением импульса, была меньше скорости света. Отсюда и из (5) следует
![]() (7)
(7)
Во-вторых, из самого смысла измерения поля в объеме V следует, что величина Δх должна быть меньше размеров пробного тела: Δx<V1/3. Учитывая (5), получим
![]() (8)
(8)
Получив эти две нижние границы для Δt, Бронштейн отмечает, что отношение первой из них ко второй
![]() (9)
(9)
«зависит от массы пробного тела, будучи совершенно ничтожной величиной в случае электрона и становясь
167
величиной порядка 1 в случае пылинки, весящей сотую долю миллиграмма». Для неопределенности ΔГ1,00 получаются соответственно две границы
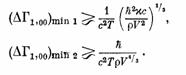 (10)
(11)
(10)
(11)
Поскольку, как видно отсюда, для возможно более точного измерения Г1,00 в данном объеме V следует применять пробные тела возможно большей массы (плотности), то существенной становится только первая граница.
Бронштейн указывает, что предыдущие рассуждения аналогичны соответствующим рассуждениям в квантовой электродинамике (при этом ссылается на свою заметку 1934 г. ) и пишет: «Но на этом месте приходится принять во внимание обстоятельство, из которого обнаруживается принципиальное различие между квантовой электродинамикой и квантовой теорией гравитационного поля. Различие это заключается в том, что в формальной квантовой электродинамике, не учитывающей структуры элементарного заряда, нет никаких принципиальных причин, ограничивающих увеличение плотности ρ. При достаточно большой плотности заряда пробного тела точность измерения компонент электрического поля может быть сделана какой угодно. В природе, вероятно, существуют принципиальные ограничения плотности электрического заряда (не больше одного элементарного заряда на объем с линейными размерами порядка классического электронного радиуса), однако эти ограничения не учитываются формальной квантовой электродинамикой. . . Не то — в квантовой теории гравитационного поля: она должна считаться с ограничением, вытекающим из того, что гравитационный радиус пробного тела (κρV) не может превосходить его действительных линейных размеров
![]() (12)
(12)
Если это учесть, то (10) дает «абсолютный минимум неопределенности»
![]()
168
Конечно, этот «абсолютный предел вычислен очень грубо, потому что при достаточно большой массе измерительного прибора начнут, вероятно, играть роль отступления от принципа суперпозиции. . . »; однако Бронштейн считает, что «аналогичный результат сохранится и в более точной теории, так как он нисколько сам по себе не вытекает из принципа суперпозиции, а соответствует лишь тому факту, что в общей теории относительности не может существовать тел сколь угодно большой массы при заданном объеме. В электродинамике нет никакой аналогии этому факту. . . вот почему квантовая электродинамика возможна без внутренних противоречий». Указав, что в теории гравитации «это внутреннее противоречие никак не может быть обойдено», Бронштейн пришел к выводу:
«В области общей теории относительности, где отклонения от "евклидовости" могут быть сколь угодно велики. . . возможности измерения еще более ограничены, чем можно заключить из квантово-механических перестановочных соотношений» и «без глубокой переработки классических понятий кажется едва ли возможным распространить квантовую теорию гравитации также и на эту область» [30, с. 276] .
Именно так впервые были обнаружены границы применимости общей теории относительности — неквантовой релятивистской теории гравитации.
Само существование таких границ предвиделось и раньше — вспомним замечание Эйнштейна 1916 г. о том, что квантовая теория должна модифицировать теорию гравитации, неудовлетворенность Эйнштейна тем, что «линейки и часы», используемые в построении ОТО, рассматривались безо всякого учета их микроскопического строения, упоминавшееся замечание Клейна 1927 г. Однако все такие соображения имели логический или методологический характер. Бронштейновский анализ проведен на физическом, количественном языке.
в) Планковские масштабы в cGћ-физике.
Нынешнему читателю в этом анализе не хватает только так называемых планковских величин, которые в наши дни появляются во всяком обсуждении квантовых границ ОТО. Эти величины представляют собой комбинации из фундаментальных констант с, G и ћ вида
![]()
169
и могут иметь любые размерности (длины, времени, плотности и т. д. ). Именно планковские величины сопоставляются границам ОТО, обусловленным необходимостью ее квантового обобщения.
При этом аргументы, приводимые в обоснование, весьма различны — от эскизов будущей теории квантовой гравитации до соображений размерности. А так как последние не требуют каких-либо сложных построений, можно предположить, что квантово-гравитационная роль планковских величин была известна очень давно, чуть ли не самому Планку [124—125].
Однако в действительности эти величины Планк ввел, безо всякой связи с квантовой гравитацией, в 1899 году, когда еще не было и самой квантовой теории. Он предложил «естественные единицы измерения», которые «обязательно сохраняли бы свое значение для всех времен и для всех культур, в том числе и внеземных и нечеловеческих» [254, с. 232]:
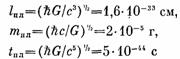 (13)
(13)
(использованы современные обозначения и величины констант). Выпишем еще выражение для планковской плотности
![]()
определяющей квантово-гравитационную эпоху в космологии.
В явном виде на квантово-гравитационное значение планковских величин было указано лишь в середине 50-х годов почти одновременно несколькими физиками — О. Клейном, Л. Д. Ландау, В. Паули и Дж. Уилером (об истории планковских величин см. [168, гл. 5]). Однако неявно такие величины есть, конечно, уже у Бронштейна, поскольку в его анализ вовлечены все три константы: с, G и ћ. Его рассуждения легко дополнить так, чтобы планковские величины возникли и явным образом. Собственно, одна такая величина — планковская масса — появилась уже в тексте Бронштейна. Это та самая «пылинка, весящая сотую долю миллиграмма», для которой неопределенности (7) и (8) имеют одинаковый порядок (в статье [30] выписано даже явное выражение для планковской массы).
170
Чтобы планковские величины «проявились», можно рассуждать так. Будем стремиться измерять гравитационное поле не только с наименьшей неопределенностью, но и в наименьшем возможном объеме, стремясь определить «поле в данной точке». Тогда уже придется рассматривать обе границы (7), (8), а не только первую из них. Для уменьшения неопределенности Г1,00 надо использовать максимальную возможную плотность пробного тела; в силу (12) это
![]()
Тогда границы (7), (8) превращаются в
![]() (7а) (8а)
(7а) (8а)
По самому смыслу измерения напряженности, усредненной за промежуток времени Т, должно выполняться условие Δt<T. Поэтому при данном Т следует стремиться к наименьшему возможному Δt. Так как τ1 уменьшается с уменьшением V, а τ2 растет, минимальное значение наибольшей из величин τ1, τ2 достигается при τ1=τ2. Тогда
![]()
При этом соответствующие размеры пробного тела
![]()
его масса
![]()
и, наконец, минимальная неопределенность напряженности гравитационного поля Г
![]()
Если же мы учтем, что неопределенность в измерении гравитационного поля следует оценивать по суммарному воздействию на пробное тело — работе напряженности на расстоянии порядка размеров тела Δg≡ΔГ∙V1/3 (эта же величина описывает неопределенность метрики), то получим
![]()
Таким образом, область применимости классической теории гравитации и пространства-времени ограничивается действительно планковскими величинами.
171
Чтобы получить планковские масштабы для квантово-гравитационных явлений, не обязательно привлекать анализ измеримости, как Бронштейн в 1935 г., или фейнмановский интеграл, как Уилер в 1955 г. Достаточно простейшим способом ввести в рассмотрение константы с, G и ћ. Можно это сделать уже на уровне физики 1913 г. Рассмотрим две точечные частицы массы М, связанные гравитационным взаимодействием и движущиеся по круговой орбите радиуса R. Подчиним эту систему классической механике Ma=Mv2/R— =GM2/(2R)2 и квантовому постулату Бора 2MvR=nћ, n=1, 2,. . . Чтобы выяснить, при каких значениях параметров М и R описание системы должно существенно учитывать квантово-релятивистские эффекты, нужно положить, что п достаточно близко к единице и скорость v достаточно близка к скорости света с. Тогда легко получить, что квантово-гравитационной области соответствует одновременная близость М и R к планковским значениям. Однако при этом глубокий пространственно-временной смысл cGћ-границ остается, конечно, незаметным.
г) Восприятие квантово-гравитационных границ.
Если бы даже в 30-е годы были известны планковские характеристики квантово-гравитационных границ, решиться тогда говорить о них было нелегко. Ведь величины 10-33 см и 10-5 г (=1019 ГэВ) фантастически далеки от насущных для физики того времени величин ядерных масштабов 10-13 см и 1 ГэВ.
Вот что писал в 1930 г. Гейзенберг: «Часто высказывается надежда, что квантовая теория после разрешения только что названных проблем [связанных с релятивистской формулировкой квантовой теории], может быть, снова будет в значительной степени сведена к классическим понятиям. Но даже поверхностный взгляд на развитие физики за последние тридцать лет показывает нам, что скорее, наоборот, можно ожидать еще более широких ограничений классического мира понятий. В добавление к изменениям нашего обыкновенного пространственно-временного мира, которые были потребованы теорией относительности и для которых характерна постоянная с, и к соотношениям неопределенности квантовой теории, символом которых может служить планковская постоянная ћ, появятся еще другие ограничения, стоящие в связи с универсальными
172
постоянными е, μ [масса электрона], М (масса протона)» [158, с. 79].
Это высказывание вполне отражало общественное мнение в физике 30-х годов. Если же в прогнозе Гейзенберга вместо е, μ, M подставить G, то это едва ли нашло бы сочувствие у кого-нибудь в те годы. В частности, потому, что тогда не было идей, которые могли хотя бы эскизно соединить величины 10-33 см и 10-13 см (такие идеи появились только совсем недавно [262]). Но, как следует из бронштейновского анализа и в соответствии с общим взглядом на теоретическую физику через магический cGћ-куб (см. разд. 5. 3), для замены набора с, ћ, е, μ, М на с, G, ћ основания были.
Видя эти основания и доверяя своему зрению, Бронштейн в подробном изложении своей работы [31] уточнил, глубокая переработка каких понятий потребуется в полной квантовой теории гравитации:
«Устранение связанных с этим [с принципиально ограниченной измеримостью гравитационно-геометрических величин] логических противоречий требует радикальной перестройки теории и, в частности, отказа от римановой геометрии, оперирующей, как мы здесь видим, принципиально не 13 наблюдаемыми величинами — а может быть, и отказа от обычных представлений о пространстве и времени и замены их какими-то гораздо более глубокими и лишенными наглядности понятиями. Wer's nicht glaubt, bezahlt einen Taler».
Пафос фундаментального вывода уравновешивается немецкой фразой, весьма необычной для ЖЭТФа. Этой фразой («Кто не верит, тот платит талер») кончается и сказка братьев Гримм «Про умного портняжку», в которой говорится о совершенно невероятных (даже по сказочным стандартам) деяниях портняжки, который «был человек на вид неказистый и порядочный растяпа, да и в ремесле своем не искусник». В художественном переводе фраза звучит так: «А кто сказке моей не верит, пусть талер дает живей!» [175, с. 334].
Появление немецкой поговорки на страницах ЖЭТФа может сказать нам кое-что о самом Бронштейне — о его эмоциональной интеллектуальности, органичной самоиронии, независимости (разве положено последовательность выкладок завершать поговоркой?).
13 В оригинале отсутствует «не» – явная опечатка.
173
Но в этом расширении обычного словаря теоретика можно усмотреть и тогдашнее умонастроение его коллег.
Теоретики уже успели привыкнуть к прорицаниям, грозящим революцией пространству-времени. И, как бывает с предсказаниями, которые не спешат сбываться, они уже надоели. В 1935 г. ожидание фундаментальных перемен не сковывало теоретиков, как в начале 30-х. Экспериментальные открытия (нейтрон, позитрон) и теория Ферми (узаконившая нейтрино) дали физике микромира обширное поле деятельности. И в этих обстоятельствах, чтобы вновь провозгласить неизбежность перестройки пространственно-временных понятий, требовалось известное мужество. У Матвея Петровича Бронштейна оно было.
Только спустя десятилетия вывод Бронштейна стал признан, хотя и сейчас еще квантовая «радикальная перестройка» теории гравитации остается нерешенной задачей.
Квантовые границы ОТО обнаружил вновь в 1955 г. Уилер, два года спустя в связи с этим вспомнили о планковских величинах [167]. В наше время планковские величины — стандартный синоним квантовой гравитации, «очевидные» границы ОТО. Еще более очевидно сейчас само существование таких границ. Однако дело обстояло совсем иначе в 30-е годы.
Бронштейн относился к анализу измеримости достаточно серьезно, поскольку в кратком изложении своей работы, существенно сократив другие разделы, анализ измеримости дал практически полностью. Но другие физики восприняли его результат о принципиальной квантовой ограниченности ОТО без должного понимания. Например, Фок, реферируя статьи Бронштейна [30, 31], нашел для этого результата лишь весьма неопределенные слова: «развиты некоторые соображения об измеримости поля» [276]. Выступая на защите и высоко оценив работу в целом (см. также [275, 278]), он скептически отнесся к анализу измеримости, усматривая прямую аналогию между нелинейностью ОТО и нелинейностью электродинамики Борна—Инфельда и сопоставляя гравитационный радиус в ОТО радиусу электрона в теории Борна—Инфельда [173, с. 318]. Отвечая на это замечание, Бронштейн в такой аналогии усомнился и был, конечно, ближе к истине.
Между нелинейной теорией гравитации (ОТО) и нелинейной электродинамикой Борна—Инфельда есть
174
глубокое различие. Нелинейность ОТО в большой степени однозначна, и физическая причина этой нелинейности — принцип эквивалентности. А нелинейный лагранжиан Борна—Инфельда «сделан руками»:
![]()
здесь LM — обычный максвелловский лагранжиан, ε — малая константа. Сам тип нелинейности не следовал из каких-либо глубоких физических соображений. Теория Борна—Инфельда была нацелена специально на проблему бесконечной собственной энергии электрона, а лагранжиан выбирался так, чтобы этой проблемы не возникало уже на классическом уровне. При этом радиус электрона rе=е2/тс2 появлялся только как характерное расстояние, начиная с которого поведение поля E~е/(r4+re4)1/2 существенно отклоняется от кулоновского.
Поэтому действительно нельзя согласиться с Фоком в том, что имеется аналогия между радиусом электрона в теории Борна—Инфельда и гравитационным радиусом, существование которого связано с фундаментальным физическим фактом — равенством гравитационной и инертной масс, или теоретическим выражением этого факта — принципом эквивалентности.
Роль принципа эквивалентности можно продемонстрировать, сопоставляя мысленные эксперименты по измерению электромагнитного и гравитационного полей.
Вернемся к итоговой формуле для неопределенности поля из п. а):
![]()
здесь ρ и μ — плотности заряда и массы пробного тела, Δx — его размер. Эта формула оправдывает понятие «электромагнитное поле в точке». Однако оправдание достигается за счет возможности использовать пробное тело с произвольно большими и независимыми плотностями заряда и массы. Такая возможность физически, конечно, фиктивна, поскольку неизвестно даже мысленных процедур изготовления соответствующих пробных тел; но теоретически эта идеализация допустима, потому что внутри самой электродинамики для нее нет запрета (значения элементарного электриче-
175
ского заряда и массы элементарных частиц вводятся в электродинамику извне).
Однако при переходе к гравитации такой запрет появляется. Его можно сформулировать по-разному. Например, ясно, что нельзя независимо распоряжаться величинами плотности «гравитационного заряда» и плотности массы, потому что имеется связь
![]()
Эта связь составляет суть принципа эквивалентности, на котором основана ОТО. И именно эта связь делает невозможным уменьшение неопределенности гравитационного поля ΔГ вместе с уменьшением размеров пробного тела Δx→0. Бронштейн такой запрет связал с невозможностью существования пробного тела с размерами, меньшими его гравитационного радиуса.
А проще всего (хотя и не так убедительно) попытаться перенести в теорию гравитации замечание Бора—Розенфельда [121, с. 121]: «. . . возникающие здесь разнообразные проблемы могут быть рассмотрены раздельно в силу того, что сам по себе аппарат квантовой электромагнитной теории независим от тех или иных представлений об атомном строении материи. Последнее явствует уже из того, что из числа универсальных констант в него входит помимо скорости света только квант действия; а из этих двух констант, очевидно, еще нельзя составить какую-либо характерную длину или интервал». В релятивистской квантовой гравитации должны действовать три фундаментальные константы с, G и ћ, из которых уже можно составить характерную длину lпл=(ћG/с3)1/2.
К анализу пределов применимости ОТО, проведенному Бронштейном, не следует предъявлять претензии в недостаточной строгости. Точное описание области применимости ОТО даст только анализ в рамках (еще несуществующей) полной квантовой теории гравитации.
И в наше время проблема измеримости гравитационного поля, так же как и гравитационное излучение атомных электронов, о котором говорил Эйнштейн, отнюдь не являются задачами практического значения. Однако, когда речь идет, по выражению Эйнштейна, о внутреннем совершенстве теории, физик имеет право рассматривать все возможности, не запре-
176
щенные самой теорией. Поскольку в теории гравитации нет запретов на рассмотрение атома и квантовых систем вообще, то величина эффекта не имеет значения для анализа теории средствами самой теории. И мысленный эксперимент по измеримости гравитационного поля — это, конечно, лишь некоторый способ анализировать внутреннее совершенство теории14. Однако история физики показывает, что именно теории высокого внутреннего совершенства достигали особенно значительного внешнего оправдания, преобразуя технику и жизнь человеческого общества в целом.
В настоящее время задача квантования гравитации не стоит изолированно. Без ее решения вряд ли будет построена единая теория фундаментальных взаимодействий. Так что дорога, на которую в 30-е годы вступил Матвей Петрович Бронштейн, вела в самый центр исследований современной физики.
5. 5. Физика и космология
В мартовском выпуске ЖЭТФа за 1937 г. в последний раз появились работы М. П. Бронштейна. Их было две. Одна содержала ядерно-физический расчет, выполненный по просьбе И. В. Курчатова; появление этой небольшой работы отражало, можно сказать, научный быт Матвея Петровича, его вовлеченность в окружающую научную жизнь. Другая, большая статья «О возможности спонтанного расщепления фотонов», отражала скорее научное бытие автора. По содержанию она относится к квантовой теории поля, или — более поздним языком — к физике элементарных частиц, однако главный смысл она обретала в космологии. Эта работа представляет собой первый реальный результат взаимодействия физики элементарных частиц и космологии, взаимодействия, столь характерного для нашего времени, когда из космологических наблюдений извлекаются свойства
14 Разумеется, Бронштейна занимало не только совершенство теории, но и ее оправдание. На защите диссертации В. К. Фредерикс спросил его, в чем могло бы проявиться гравитационное излучение. Бронштейн указал на эффект замедления вращения двойных звезд [173, с. 319]. Этот ответ, прозвучавший в 1935 г., стоит сопоставить с первым наблюдательным, хотя и косвенным свидетельством существования гравитационного излучения. Именно такой эффект обнаружен в 1979 г. в двойном пульсаре.
177
элементарных частиц, а космологические модели (или сценарии, как сейчас говорят) строятся на основе теории элементарных частиц. В 30-е годы ситуация была совершенно другой, и для того чтобы лучше понять работу Бронштейна, надо знать тогдашнее состояние космологии.
а) Космология в 30-е годы.
С момента своего возникновения в 1917 г. и до конца 20-х годов релятивистская космология воспринималась в основном лишь как волнующая возможность физико-математического описания Вселенной и как демонстрация огромного потенциала и глубины общей теории относительности. Реальных способов проверить космологическую теорию не было — даже проверки основ ОТО были на пределе экспериментального искусства и имели невысокую точность. Чисто теоретический характер космологии и неединственность модели Вселенной позволяли относиться к космологии с «ласковой снисходительностью», как к многообещающему, но слишком еще юному созданию.
В конце 20-х годов положение круто изменилось. В результате астрономических наблюдений (в первую очередь Э. Хаббла) была надежно установлена внегалактическая природа так называемых спиральных туманностей, которые оказались просто другими галактиками. И межгалактическое расстояние стало космологическим масштабом, по отношению к которому только и можно говорить об однородности Вселенной (без этого условия не удается получать достаточно определенные космологические выводы из уравнений ОТО).
А главный результат, который в 1929 г. получил Хаббл, изучая другие галактики, состоял в открытии систематического красного смещения их спектров, пропорционального расстоянию
![]() (14)
(14)
В астрономии единственным способом определять скорость далеких объектов была доплеровская интерпретация смещений их спектров v/c=Δλ/λ (если v<<с). Поэтому не потребовалось усилий, чтобы записать соотношение Хаббла как зависимость скорости удаления галактик от их расстояния до наблюдателя (до нашей Галактики):
![]() (15)
(15)
178
Коэффициент H Хаббл получил в результате измерений и введения многоступенчатой шкалы расстояний; по его тогдашним данным H≈(2∙109 лет)-1. Так был установлен первый наблюдательный факт космологического характера. Очень быстро обнаружилось, что в релятивистской космологии была уже заготовлена математическая модель, пригодная для описания этого факта,— нестатическая модель Фридмана 1922 г., переоткрытая Леметром в 1927 г. 15
Как следствие интерес к космологии резко возрос. Вместе с тем появилась возможность, а значит, и необходимость, количественно проверить космологическую теорию наблюдениями, т. е. отнестись к ней всерьез, как к физической теории. Одним из проявлений новой ситуации стал обстоятельный обзор по релятивистской космологии, написанный Бронштейном для УФН в 1930 г. (о нем рассказывалось в разд. 3. 6). Этот обзор автор закончил указанием на главную трудность релятивистской космологии, связанную с возрастом Вселенной. Уже наивное рассмотрение хаббловского соотношения (15) дает, что расширение Вселенной началось
T=R/V=H-1=2∙109 лет
тому назад. В точной космологической модели Фридмана—Леметра возраст Вселенной получался еще меньшим. Это вопиюще не соответствовало данным изотопной геологии (согласно которым уже для истории Земли требуется несколько миллиардов лет) и астрофизики. Только три десятилетия спустя в результате нескольких пересмотров шкалы расстояний хаббловский коэффициент H уменьшился в десять раз и соответственно возраст Вселенной стал оцениваться приемлемой величиной ~20∙109 лет. Сейчас хорошо видно, как бедны были тогдашние возможности эмпирического обоснования космологии, если основной количественный параметр изменился в десять раз. А тогда, в 30-е годы, астрономы хоть и сознавали, что данные их наблюдений весьма неопределенны, но, как это обычно бывает, меру этой неопределенности преумень-
15 Напомним, что для Эйнштейна, строившего в 1917 г. первую космологическую модель, однородность распределения вещества была гипотезой, а малые относительные скорости звезд (!) — «самым важным из всего, что нам известно из опыта о распределении материи» [306, с. 608].
179
шали. У нынешних специалистов может вызвать улыбку то, что Хаббл, стремившийся к интерпретации наблюдательного материала в рамках ОТО, пытался привлечь модель с положительной кривизной пространства.
Тридцатые годы были тяжелым испытанием для релятивистской космологии не только из-за принятой тогда короткой шкалы расстояний. Само несоответствие теории наблюдениям стало одной из причин появления альтернативных космологических схем (чтобы не злоупотреблять словом «теория»). Действовали и другие причины. От грандиозной картины расширения Вселенной у некоторых, видимо, не выдерживали нервы, и они искали более простого объяснения для соотношения Хаббла. Р. Цвикки уже в 1929 г. предположил, что галактики на самом деле не удаляются, а просто фотоны, прилетающие к нам от этих галактик, за долгое время путешествия успевают покраснеть. Милн в своей «кинематической» космологии, которую начал строить в 1931 г., обходился без ОТО и отделял космологию непроницаемой стеной от атомной физики. Эддингтон, наоборот, строил фундаментальную теорию, описывающую сразу и во взаимной связи и микро-, и мегаскопические свойства Вселенной. Тогдашнюю ситуацию вполне характеризует то, что авторами еретических космологий были астрофизики первой величины — Эддингтон, Милн, Цвикки.
Для большинства физиков-теоретиков эти построения выглядели если не беспочвенными, то безответственными фантазиями16, хотя астрономы честно сравнивали с наблюдениями все пригодные для этого модели — Цвикки, Милна и Леметра (имя Фридмана тогда упоминалось редко). И космология ОТО отнюдь не выглядела тогда наилучшей с наблюдательной точки зрения.
16 Исключение, которое нельзя не упомянуть, составлял Дирак. В 1937 г. он выдвинул весьма спекулятивный проект, ради космологии отказываясь от фундаментальных положений физики. В частности, у него гравитационная константа G стала функцией времени G(t). Здесь не место обсуждать причины, по которым великий физик так далеко отошел от физики [170, 183]. Подчеркнем только, что его идея не пользовалась поддержкой коллег. И уж во всяком случае для переменной гравитационной «константы» G(t) нет места на cGћ-карте Бронштейна,
180
Отношение физиков (даже специалистов в ОТО) к релятивистской космологии также не было автоматически благоприятным. Космологическая задача слишком отличалась от других задач физики. Из ОТО надо было извлечь описание принципиально единичного объекта с принципиально единственной историей, а математический аппарат ОТО — дифференциальные уравнения и начальные условия — не отличается от других физических теорий и никакой единичности изначально не содержит. Кроме того, любое сопоставление теории с наблюдениями предполагало нефизическую экстраполяцию — ведь надо нечто говорить сразу о всей Вселенной, а не только о наблюдаемой ее части. К такой экстраполяции, в частности, скептически относился В. А. Фок.
В СССР положение космологии в 30-е годы отягчалось еще и философским давлением на естествознание. В предыдущих главах уже говорилось о тогдашней повышенной чувствительности идеологии к естествознанию, о дискуссиях вокруг теории относительности и квантовой механики. По отношению к физическим теориям стражи философского порядка покушались только на отдельные следствия и интерпретации — слишком явным было практическое значение физики. Что же касается космологии, то скромные ее достижения не препятствовали отвергать ее целиком. Уже обзор Бронштейна 1931 г. в УФН был снабжен, напомним, нелепыми философскими примечаниями. А к 1937 г., когда появилась последняя статья Бронштейна, ситуация еще более обострилась. Те философы, которые считали себя вправе надзирать за физиками, особенно предосудительным считали возможную пространственную конечность Вселенной и ее нестатичность; гораздо более приемлемым казалось покраснение фотонов. Этих философских надзирателей помимо физической безграмотности отличал философский догматизм, следовать которому всегда спокойней и безопасней. Не обошлось тут без уже знакомого нам борца против физического идеализма: «На фронте космологии» — так назвал В. Е. Львов свою крупнокалиберную статью, вполне дающую представление об аргументации противников релятивистской космологии. В этой статье не хватает, пожалуй, только политической интерпретации покраснения фотонов; такой аргумент встал бы рядом с крас-
181
ным цветом меридиана у другого тогдашнего борца против идеализма — В. Ф. Миткевича.
«Философские» атаки достигали цели. Иначе не понять такую фразу из статьи Ландау 1937 г. : «. . . чтобы поддерживать солнечное излучение на постоянном уровне в течение двух миллиардов лет (предположительного времени существования Солнца согласно общей теории относительности). . . » [216] (конечно, здесь подразумевается хаббловская оценка возраста Вселенной). Иначе появилась бы вторая часть обзора Зельманова «Космологические теории» [184], которая должна была включать релятивистскую космологию.
В такое время и появилась статья Бронштейна, показавшая, что гипотеза покраснения фотонов должна быть отвергнута. В результате доплеровская интерпретация красного смещения, лежащая в основе нестатической космологии, получила физическое обоснование. Поводом для этой работы Бронштейна стало то, что предположение о покраснении фотонов, выглядевшее произвольной гипотезой (во всяком случае в глазах М. П. ), получило неожиданную поддержку со стороны новейшей фундаментальной физики — дираковской теории электрон-позитронного вакуума.
В 1933 г. О. Гальперн высказал гипотезу, что в пустом пространстве фотон может взаимодействовать с электронами, находящимися в состояниях с отрицательной энергией, в результате чего электроны переходят в состояния с положительной энергией и затем возвращаются в исходное в несколько шагов, испуская кванты меньшей энергии. «Рассеяние такого типа,— писал Гальперн,— может только уменьшить частоту; это уменьшение, если оно мало, было бы в среднем пропорционально расстоянию, проходимому квантом через «вакуум». В этой связи может быть упомянута гипотеза, что константа Хаббла сводима к атомным константам без использования гравитационных теорий» [142]. Гальперна поддержал в 1936 г. Гайтлер в своей известной книге — первой монографии по квантовой электродинамике [141, с. 193] (видимо, именно книга Гайтлера была непосредственным поводом для работы Бронштейна, краткое изложение которой [34] появилось в 1936 г. )
Такая возможность фундаментальной физикой объяснить главный факт космологии заслуживала, конечно, того, чтобы рассмотреть ее внимательно. Нет основа-
182
ний думать, что в отрицательном результате Бронштейн был уверен заранее. В частности, потому, что он отнюдь не считал окончательной релятивистскую космологию в тогдашней ее форме.
б) Отношение М. П. Бронштейна к космологии.
Уже в обзоре Бронштейна 1931 г. наряду с энтузиазмом от могущества физической теории, способной описывать Вселенную, чувствуется трезвый взгляд. Тогда, правда, главной трудностью космологии Бронштейн называл неувязку хаббловского возраста Вселенной с данными астро- и геофизики; владея материалом этих областей, он не мог закрыть глаза на это расхождение. Однако в следующие несколько лет центром космологических размышлений Бронштейна стала принципиальная теоретическая трудность релятивистской космологии — множественность космологических моделей, проблема выбора начальных условий. Бронштейн считал, что подлинная космологическая теория должна не просто подыскать подходящую модель из числа многих возможных, а объяснить однозначным образом фундаментальные свойства — принципиально единственной — Вселенной как целого: в частности, объяснить, «почему из двух возможностей (расширение и сжатие) вселенная выбрала именно первую» [21, с. 28], объяснить безразмерные константы, характеризующие Вселенную. Бронштейн считал, что эти задачи неразрешимы в рамках неквантовой ОТО, уравнения которой симметричны по отношению к прошедшему и будущему, что решить их можно будет только на основе полной физической cGћ-теории: «на самые существенные вопросы о мире как о целом мы вынуждены пока ответить незнанием, и физическая теория еще должна будет пройти длинный и трудный путь, прежде чем эти вопросы смогут быть надлежащим образом поставлены и разрешены» [Там же, с. 30].
Эту позицию можно было бы назвать максималистской, учитывая, что в космологии за прошедшие полвека решалось и решается сейчас много осмысленных задач (если их не относить к математике и космогонии), но нынешнее состояние космологии позволяет видеть глубинную правоту М. П. Бронштейна [181]. В космологических размышлениях Бронштейна присутствовал мотив, имеющий любопытные продолжения в современной космологии. Как известно, о Вселенной в целом и о (фундаментальной для космоло-
183
гии) экстраполяции физических законов на всю Вселенную Эйнштейн заговорил не первым. В наследство от классической термодинамики и статистической физики космология получила вопрос о пределах применимости второго начала термодинамики, «тепловую смерть Вселенной» и флуктуационную гипотезу Больцмана, предназначавшуюся для спасения Вселенной от этой унылой смерти. Больцман предположил, что наш наблюдаемый Мир — это гигантская флуктуация в равновесной и в среднем «мертвой» Вселенной; вероятность таких флуктуации очень мала, но сами они неизбежны. Соответствующий круг вопросов горячо обсуждался в больцмановские времена, хотя для этого обсуждения слов в физико-математическом языке не хватало.
Рассматривая эти же вопросы, Бронштейн пришел к выводу, что гипотеза Больцмана должна быть отвергнута из-за чудовищно малой вероятности такой флуктуации и что «объяснение вселенной как целого не может быть достигнуто на основе законов, симметричных по отношению к прошедшему и будущему, по отношению к замене +t на —t; во вселенной должны существовать по крайней мере отдельные области, которые подчиняются законам, асимметричным по отношению к прошедшему и будущему» [21, с. 14]. В 1933 г. такие «отдельные области» легко сопоставлялись с «патологическими областями» внутри звезд (Ландау, 1932), где должна была действовать сћ-теория и, согласно Бору, мог не действовать закон сохранения энергии. Однако бронштейновский анализ космологической проблемы не зависел от идеи Бора. Уверенность Бронштейна в том, что Вселенную как целое может объяснить только несимметричная по времени теория, привела его к убеждению, что полная сGћ-теория должна быть несимметрична по времени. Современная космология не может обойтись без T-не-симметричных физических теорий, с помощью которых объясняют, в частности, барионную асимметрию Вселенной [181].
Что касается флуктуационной гипотезы Больцмана и ее опровержений на основе вероятностных соображений, то им до сих пор не удалось придать форму, достаточно определенную и, главное, приложимую к релятивистской космологии. Однако Бронштейн и Ландау внесли в обсуждение новый элемент. Они придума-
184
ли следующий остроумный довод в защиту флуктуационной гипотезы и его опровержение.
На вопрос, как это человеку (человечеству) так невероятно повезло — наблюдать столь большую флуктуацию, можно было бы ответить, пишет Бронштейн, что для самого существования человека необходимы условия, которых не найти в равновесной, термодинамически мертвой части Вселенной: «Для того чтобы мы могли наблюдать какое-либо событие, нужно, чтобы мы при этом могли существовать; существование же жизни связано с целым рядом условий, и, вероятно, к числу необходимых условий относится наличие твердой планеты, нагреваемой Солнцем, и т. д., т. е. уже наличие весьма значительных отступлений от термодинамического равновесия» [21, с. 13]. Но такой качественный ответ не выдерживает количественной проверки: для существования человека было бы достаточно места, если бы флуктуация затронула область, простирающуюся только до ближайших звезд (~1040 км3), а не всю наблюдаемую Вселенную (~1066 км3). Отношение соответствующих объемов характеризует степень невероятности гипотезы Больцмана.
Даже если не говорить о необходимости использовать в космологии релятивистскую теорию гравитации, эти рассуждения уязвимы. Для существования наблюдателя, подобного человеку, в течение некоторого времени может хватить помещения и гораздо меньших размеров, чем межзвездные. Но для возникновения наблюдателя, подобного человеку, эта область может оказаться тесной. Ясно, что вероятность флуктуации, состоящей в появлении человека (и окружающей его живой природы) сразу в готовом виде, отличается от вероятности простейшей флуктуации, способной стать началом эволюционной цепи, ведущей к человеку, отличается множителем, несравненно меньшим, чем 10-26. Поэтому надо позаботиться о спокойных условиях для эволюции в течение достаточно длительного времени Т, т. е. нужно побеспокоиться о достаточно спокойном окружении места эволюции на расстоянии сТ. Если время биоэволюции, приведшей к человеку (~109 лет), достаточно представительно, то получается как раз область размерами порядка наблюдаемой Вселенной.
Нетрудно понять, что неопределенность контрдовода не меньше неопределенности исходного довода. Одна-
185
ко уже в исходном фигурирует необычная для физики генетическая связь объекта и наблюдателя, порожденного самим объектом. Такая связь составляет суть так называемого антропного принципа, который привлекает значительное внимание в современной космологии. Эта связь (хотя и в негативном смысле) впервые, по-видимому, обсуждалась в статье Бронштейна 1933 г. [21] и в его совместной с Ландау статье [22]. Соответствующее рассуждение воспроизведено в «Статистической физике» Ландау, Лифшица [219, с. 29] (и в последующих изданиях) и стало отправным пунктом для различных «антропных» формулировок [185, 192].
Отношение Бронштейна к космологической проблеме во многом определялось его отношением к фундаментальной физической теории, поскольку по его представлениям «космологическая теория должна увенчать здание физической теории вообще» [21, с. 29]. Общий взгляд на космологию Бронштейн излагал в 1933— 1935 гг., и максимализм этого взгляда естественно связать с характерным для тех лет ожиданием радикальных перемен в фундаментальной физике. В последующие годы его отношение к космологии стало, видимо, более уравновешенным. Однако идея глубинного родства микрофизики и космологии была укоренена в его сознании.
А теперь, в общих чертах охарактеризовав обстоятельства, в которых появилась последняя крупная работа Матвея Петровича Бронштейна, расскажем наконец о ее содержании.
в) Красное смещение, принцип относительности и поляризация вакуума.
Начинает Бронштейн с краткого обсуждения эффектов нелинейного самодействия в электродинамике. О «рассеянии света на свете» тогда заговорили и в рамках классической нелинейной (Борн — Инфельд), и в рамках квантовой электродинамики. Превращение фотона в пустом пространстве в несколько других, или спонтанное расщепление фотона,— это родственный эффект; если в уравнении рассеяния γ1+γ2→ →γ3+γ4 один фотон «перенести с обратным знаком» из левой части в правую, получим уравнение расщепления фотона γ→γ1+γ2+γ3 Но, как отмечает Бронштейн:
«С точки зрения экспериментатора эффект спонтанного расщепления фотона мог бы представлять несравненно больший интерес, нежели рассеяние света све-
186
том. Проверка на опыте теоретических расчетов, относящихся к рассеянию света светом, в настоящее время практически невозможна, так как для этого потребовались бы чудовищные интенсивности в условиях полного исключения всякого добавочного рассеяния. Для того же чтобы наблюдать спонтанное расщепление фотона, если оно на самом деле происходит, необходимо лишь иметь в своем распоряжении достаточно большие промежутки времени: как бы ни была мала вероятность спонтанного расщепления в секунду, расщепление должно произойти, если только фотон путешествует в пустоте достаточно долгое время. В распоряжении астронома имеются фотоны, распространявшиеся в пустом пространстве в течение огромного промежутка времени (свет от внегалактических туманностей 20-й звездной величины, спектры которых еще могут быть сфотографированы с помощью стодюймового рефлектора, доходит до земного наблюдателя в течение 190 миллионов лет). Нельзя ли попытаться решить вопрос о спонтанном расщеплении фотонов с помощью астрономического наблюдения?» [35, с. 285].
Не так давно стали говорить о том, чтобы в качестве физической лаборатории использовать Вселенную (из-за физических и экономических ограничений на создание все более мощных ускорителей) [242]. Мы видим, что эта идея была хорошо знакома Бронштейну в 1937 г. Вернемся, однако, к его статье.
«Гальперн высказал гипотезу, согласно которой "космическое красное смещение", исследованное Хабблом и Хьюмасоном, объясняется постепенным отщеплением небольших инфракрасных фотонов от фотона видимого света, идущего к земному наблюдателю от отдаленных небесных объектов. Эта точка зрения кажется весьма привлекательной, так как все существующие теории красного смещения (релятивистские модели "расширяющейся вселенной", диффузия системы галактик по Милну) оказались бессильными объяснить наблюдаемое количественное значение "коэффициента экспансии". Гипотеза Гальперна дает, на первый взгляд, надежду на вычисление коэффициента экспансии системы галактик из констант атомной физики. Я думаю, однако, что гипотеза Гальперна неверна».
Это мнение Бронштейн обосновывает очень красивым рассуждением, обнаружив, что «с помощью специального принципа относительности можно вывести
187
некоторые общие свойства интересующего нас явления, не делая никаких специальных предположений о природе механизма, приводящего к спонтанному расщеплению фотона».
Пусть фотон летит в пустоте вдоль оси х относительно некоторой системы отсчета (х, t), на диаграмме Минковского (х, ct) мировая линия фотона — АВ. И пусть другая система отсчета (х', t') движется относительно
Мировая линия фотона
исходной со скоростью v тоже вдоль оси х. Если w — вероятность расщепления фотона в единицу времени, то вероятность того, что расщепление фотона произойдет между мировыми точками A и В, должна быть одинакова в обеих системах отсчета и равна
![]()
Поскольку для света хB—хА=с(tB—tA), то
![]()
Отсюда следует
![]()
188
Преобразование Лоренца дает
![]()
А поскольку по формуле эффекта Доплера
w∙(tB—tA)=w'∙(tB'—tA').
то
wν=w'ν',
т. е. произведение wν — лоренц-инвариантная величина. Считать wν просто постоянной величиной, как показывает Бронштейн, нельзя в силу принципа неопределенности. Если же учитывать, что «"фотон", с которым имеет дело экспериментатор, является квантовым обобщением не классической неограниченной плоской волны, а волнового пакета, составленного из таких плоских волн и обладающего, следовательно, не вполне определенным значением количества движения», и ввести параметры реального «фотона» — спектральную ширину и неопределенность направления — с помощью неопределенности волнового вектора Δνx, Δνy, Δνz, то получим, что
![]()
где f — некоторая функция, т. е. сильную зависимость вероятности расщепления фотона от частоты. В случае, если бы красное смещение объяснялось этим механизмом, величина смещения была бы существенно разной в разных частях спектра. А по астрономическим наблюдениям смещение одинаково для всех спектральных линий одного и того же объекта, что вполне соответствует доплеровской интерпретации, согласно которой смещение зависит только от скорости объекта:
![]()
Тем самым космологическая компонента гипотезы Гальперна была «убита».
Оставалась физическая компонента. И эту компоненту можно было проверить только прямым расчетом. Таких расчетов Бронштейн выполнил, собственно, два; это было связано с тем, что, как он отмечает, «несовершенство существующей теории позитрона делает исчерпывающее теоретическое решение вопроса крайне затруднительным». Первый расчет, в рамках «элементарной теории,
189
не учитывающей взаимодействия электронов отрицательной энергии друг с другом», привел к возможности спонтанного распада фотона на три части. Однако помимо физически неполной формулировки задачи получившееся в результате выражение вероятности нелегко осмыслить физически. Второй расчет проведен уже с учетом поляризации вакуума и дал нулевую вероятность спонтанного расщепления фотона (при тогдашнем состоянии квантовой электродинамики такой расчет был трудной задачей). Так что предположение Гальперна и Гайтлера было опровергнуто окончательно.
Результат, полученный на основе общего физического принципа — специального принципа относительности,— согласовывался с прямым квантово-электродинамическим расчетом. Это согласие было существенно и для самой физической теории, потому что, как писал Бронштейн: «В настоящее время еще не существует вполне законченной теории поляризации вакуума».
Последняя работа Бронштейна — это теоретическая физика высшего класса: мастерское владение фундаментальными физическими принципами, умение с их помощью извлекать новые физически содержательные утверждения для сложных ситуаций, внимание к эксперименту и, конечно, владение техническим ремеслом теоретика.
Результат Бронштейна был замечен и оценен. Его красивое рассуждение, использующее принцип относительности, приводится, например, в известной монографии по космологии Я. Б. Зельдовича и И. Д. Новикова [183, с. 124]. Вошло оно и в арсенал фундаментальной микрофизики. В этой области время от времени появляются предположения о необычном поведении физических объектов на очень малых расстояниях (соответственно при больших импульсах), достаточно малых (больших), чтобы эта необычность не была заметна до сих пор в экспериментах. Бронштейновское рассуждение указывает существенные ограничения для гипотез такого рода. Ведь если предположить, что с фотоном, например, может «что-то» происходить при очень коротких длинах волн, когда, скажем, может чувствоваться дискретность пространства, то согласно Бронштейну это «что-то» должно помнить о своем низкочастотном (длинноволновом) хвосте, гораздо бо-
190
лее доступном эксперименту, так как
![]()
Но и Бронштейн в 1937 г. не замыкался в рамках космологии и теории вакуума (эти рамки, как ни странно это звучит сейчас, были тогда весьма узкими):
«Заметим, что общие свойства вероятности расщепления в единицу времени, выведенные выше с помощью принципа относительности, остаются справедливыми и в том случае, если в числе частей, на которые распадается фотон, имеются не только кванты света, но и гравитационные кванты. (Такие расщепления, разумеется, нисколько не противоречат законам сохранения. ) В настоящее время не существует удовлетворительной теории взаимодействия между светом и тяготением. Возможно, что будущая квантовая «единая теория поля» должна будет рассмотреть и такие превращения (полные или частичные) квантов электромагнитного поля в гравитационные кванты. «Nature seems to be delighted with transmutations» (Исаак Ньютон. «Оптика», вопрос 30)» [35, с. 290].
Трансмутации
с
участием гравитонов, о которых здесь говорится, привлекали внимание
спустя 10—
30 лет в рамках квантовой гравидинамики, но, несомненно, более важную
роль им
предстоит сыграть во псе еще будущей «квантовой единой теории поля».
Предисловие
Глава 1. Детство и юность. Путь в науку. Первые научные работы
Глава 2. В Ленинградском университете (1926-1930 гг. )
Глава 3. В Ленинградском физико-техническом институте
Глава 4. О трудных временах для законов сохранения и о трудной профессии физика-теоретика
Глава 5. cGћ-физика в биографии Бронштейна
Глава 6. Стиль творческой личности
Библиография
Приложение. Две статьи М. П. Бронштейна из журнала «Человек и природа» за 1929 год