Приложение. Две статьи М. П. Бронштейна из журнала «Человек и природа» за 1929 год

 

Всемирное тяготение и электричество (Новая теория Эйнштейна) 3

Эфир и его роль в старой и новой физике. 15

 

 

Помещенные здесь статьи помогают представить себе состояние фундаментальной физики, творческий диапазон и мировосприятие М. П. Бронштейна в начале его самостоятельного пути в науке. Дополнительное освещение рождается сходством тогдашней ситуации в теоретической физике с нынешней.

Двухнедельный научно-популярный и культурно-образовательный журнал "Человек и природа" (издававшийся в Ленинграде издательством "Красная газета") ставил своей целью знакомить широкие читательские круги с важнейшими вопросами современной науки и культуры. Так было написано на обложке журнала, и так было на самом деле.

Прежде чем кратко прокомментировать статьи Бронштейна, перелистаем годовой комплект журнала, чтобы ощутить тогдашнюю атмосферу научно-общественной жизни. На некоторых статьях глаз невольно останавливается. «Опыты оживления головы». «Проблема анатомической основы одаренности и мозг В. И. Ленина» (с сопоставлением микрофотографий среза мозга обыкновенного человека (?) и мозга Ленина). Двумя статьями и портретом на меловой бумаге отмечается 50-летие Эйнштейна. Заглавная статья одного из номеров принадлежит небезызвестному И. Презенту, который тогда еще боролся не с генетикой, а с механистическим марксизмом. В материалах, посвященных «учению об омоложении», наряду с использованием мочи беременных женщин фигурирует и метод Воронова (пересадка половых желез), упомянутый в письме Капицы из раздела 3. 9. Обсуждаются весьма разнообразные проблемы: «Задачи и перспективы звездоплавания», «Спорные вопросы марксистской экономики», «Связь исторического материализма с диалектическим».

В журнале отразилась отнюдь не застойная общественная жизнь: на январских выборах в Академию наук были забаллотированы три кандидата-коммуниста; на III Всесоюзном съезде научных работников наряду с другими проблемами го-

242

 

ворилось, что «затирание коммунистов, антисемитизм наблюдаются как прочное явление в некоторых вузах»; VII Всесоюзный съезд просвещенцев высказался за «пополнение кадров батрацкой и бедняцкой молодежью и за усиление борьбы с теми просвещенцами, которые подпадают под влияние буржуазных элементов города и села. . . »

В редколлегии журнала физику представлял Я. И. Френкель, и представлял очень успешно. Практически в каждом номере статьи по физике. Фамилии большинства авторов сейчас хорошо известны: Хвольсон, Мысовский, Харитон, Шальников, Кобеко, Курчатов, Дорфман, Кикоин, Гохберг, Гамов. Опубликованы переводы статей Планка, Комптона, Шредингера. Уже из этого перечня ясно, что на страницах журнала была представлена вся физика.

Теперь, обрисовав несколькими штрихами журнальный фон, перейдем к статьям Бронштейна.

Его рассказ в апрельском номере о «новой теории Эйнштейна» был посвящен более чем актуальному вопросу тогдашней теоретической физики. Достаточно сказать, что этот вопрос стал одним из главных на конференции по теоретической физике, собравшейся в Харькове в конце мая (рассказ Д. Иваненко об этой конференции помещен в № 14). Это первая популярная статья двадцатидвухлетнего автора (еще не закончившего, напомним, университет). Подписана она инициалами М. В., возможно, потому, что автор не решил еще, как ему относиться к самому жанру популяризации. Помимо отваги, с которой автор взялся объяснить очень высокие теоретические материи, производят особое впечатление слова о квантовой геометрии (за год до появления первых публикаций на эту тему, см. разд. 3. 4) и заключительная фраза статьи, фраза, под которой и сейчас подписались бы многие теоретики.

Вторая помещенная здесь статья настолько отличается от первой, что кажется написанной другим человеком. Там энтузиазм по поводу «последнего слова» науки, тут внимательное разглядывание предшествовавших «слов» науки, всей эволюции, вкус к историческим деталям. И все же у этих статей один автор, которому просто очень интересно связать последнее слово науки с предыдущими. Первую статью прекрасно дополняет фраза из второй: «Физические величины не могли бы быть выведены из геометрических, если бы уже каким-то образом не заключались в них; и если физика становится геометрией пространства и времени, то эта геометрия в такой же мере становится физикой». Что касается заключительного прогноза, то он неверен только лексически: слово «эфир», слишком отяго-

 243

 

щенное историей, осталось в прошлом. По существу же прогноз оправдался, поскольку понятия пространства-времени и вакуума, унаследовавшие роль эфира, играют ключевую роль в современной физике.

В первых статьях Бронштейна чувствуется, конечно, давление научного лексикона (которое со временем и с мастерством исчезнет начисто), но это не мешает видеть свободное течение мысли. А такая свобода порождается только полным владением материалом.

Чтобы не возникло ощущение, что Бронштейн интересовался исключительно супервеликими проблемами, отметим, что между помещенными здесь статьями Бронштейн опубликовал статью о японском счетном приборе «Соробан». Его интересы были широки и полнокровны.

Итак, 1929-й год, журнал «Человек и природа», 22-летний М. П. Бронштейн.

 

Всемирное тяготение и электричество (Новая теория Эйнштейна)

Человек и природа. 1929. № 8. С. 20-25.

 

Создатель теории относительности проф. Альберт Эйнштейн выступил с новой математической теорией, объединяющей в одно целое явления тяготения и электромагнитное поле. Помещены статьи, разъясняющие смысл новой теории, но вследствие их краткости они оказались недоступными пониманию среднего читателя. Для того чтобы понять новую теорию Эйнштейна, необходимо уяснить себе основы общей теории относительности, так как новая теория является непосредственным продолжением и развитием идей Эйнштейна о тяготении, резюмированных им в общей теории относительности. Трудность понимания этих идей происходит от двух причин. Первой причиной является то, что теория Эйнштейна оперирует не с обычным трехмерным пространством и рассматриваемым отдельно от него временем, а с четырехмерной совокупностью пространства и времени, рассматриваемым как некоторое четырехмерное «пространство». Точками такого четырехмерного пространства являются не обычные пространственные точки, а так называемые «события», т. е. точки пространства, рассматриваемые в определенный момент времени. Весь мир теории относительности является четырехмерной совокупностью таких «событий», охватывающей собою прошлое, настоящее и будущее.

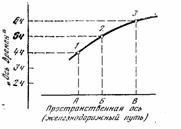
Получить наглядное представление об этом четырехмерном слиянии пространства и времени возможно при рассмотрении более простого случая, когда пространство, соединяемое с временем, было первоначально не трехмерным, а одномерным. Примером может служить хотя бы такая известная всем вещь, как график железнодорожного движения. Проведем на листе бумаги две взаимно перпендикулярные прямые (оси координат). Первая прямая представляет изображение железнодорожного пути, вторая является той осью, на которой откладываются в известном масштабе проме-

245

 

жутки времени. Рассмотрим какую-нибудь точку этой диаграммы, например обозначенную цифрой 1 (рис. 1). Опустим из этой точки перпендикуляры на обе оси. Перпендикуляр, опущенный на ось, изображающую железнодорожный путь, пересечет ее в точке А, а перпендикуляр, опущенный на ось времен, пересечет ее в точке, соответствующей какому-нибудь определенно-

 

 

му моменту времени, например 4 часам пополудни. В этом случае говорят, что точка 1 соответствует событию, происходящему в 4 часа пополудни в точке А железнодорожного пути. Если по железнодорожному пути перемещается поезд, то на диаграмме возможно начертить линию, точки которой соответствуют событиям, заключающимся в прохождении поезда в определенные моменты времени через определенные места железнодорожного пути. Такая линия начерчена на рисунке. Из нее видно, что в 4 часа пополудни поезд был в точке A, в 5 часов пополудни он был в точке Б (это «событие» изображается на диаграмме точкой 2) и т. д. Построение железнодорожных графиков известно каждому школьнику. Легко видеть, что если поезд двигался по железнодорожному пути с постоянной скоростью, то график его движения изобразится на диаграмме прямой линией, если же он двигался не равномерно, то графиком будет служить кривая или ломаная линия.

Четырехмерная совокупность «событий», рассматриваемая в теории относительности Эйнштейна и введенная впервые в эту теорию знаменитым математиком Германом Минковским, представляет полную аналогию с железнодорожным графиком, с той лишь только разницей, что эта четырехмерная совокупность

246

 

по вполне понятным причинам не может быть изображена графически. Изучающий теорию относительности должен мыслить таким образом, что вместо движения материальной точки в трехмерном пространстве по некоторому пути он сразу представляет себе линию, являющуюся графиком движения этой материальной точки в четырехмерной «диаграмме» Эйнштейна. Подобные представления о четырехмерной совокупности «событий» были развиты Минковским и Эйнштейном уже для «специальной теории относительности», в которой явления тяготения еще не рассматривались. Когда Эйнштейн начал работать над созданием новой теории тяготения (в 1912 г. ), ему пришлось ввести новое большое усложнение. Этим усложнением было введение неевклидовой геометрии.

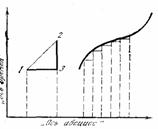
Рассмотрим вкратце, в чем здесь дело, и будем для простоты рассматривать снова не четырехмерную совокупность точек, с которой приходится иметь дело в теории Эйнштейна, а двухмерную, которую возможно изобразить на листе бумаги. Проведем снова две взаимно перпендикулярные оси координат и рассмотрим две точки 1 и 2 на этой диаграмме (рис. 2). Расстояние между точками 1 и 2 можно вычислить с помощью теоремы Пифагора, если даны так называемые «проекции отрезка 1 2 на координатные оси», т. е. катеты прямоугольного треугольника 123, проведенные параллельно координатным осям. Квадрат длины отрезка 1 2 равен сумме квадратов его проекций 1 3 и 2 3. Теорема Пифагора даст возможность вычислять длину также и любой кривой линии, проведенной на диаграмме. Для этого нужно разбить кривую линию на ряд таких мелких частей, что каждая из этих частей может приближенно рассматриваться как отрезок прямой линии (бесконечно малая дуга может быть заменена своей хордой). Вычислив длину каждого бесконечно малого отрезка прямой линии, равную квадратному корню из суммы квадратов проекций этого отрезка, мы можем сложить полученные результаты и найти таким образом длину всей кривой линии. Такое вычисление длины кривой, опирающееся на теорему Пифагора, является необходимым следствием геометрии Евклида.

Неевклидова геометрия, начало созданию которой положили сто лет тому назад Лобачевский, Гаусс и Болиаи и которая была приведена в более совершен-

247

 

ную форму гениальным немецким математиком Берн-хардом Риманом, представляет непосредственно обобщение геометрии Евклида. Вместо того чтобы вычислять квадратный корень из суммы квадратов проекций бесконечно малого отрезка, как это делается в геометрии Евклида, неевклидова геометрия вычисляет квадратный корень из более сложного выражения, являющегося суммой не только квадратов бесконечно малых проекций, но и произведения этих проекций, причем в этой сумме каждый квадрат и произведение предварительно умножается на некоторый коэффициент. Таким образом, евклидова геометрия является тем частным случаем неевклидовой геометрии, который получится, если коэффициенты при квадратах проекций равны единице, а коэффициенты при произведении равны нулю. В неевклидовой же геометрии эти коэффициенты могут принимать различные значения в разных точках пространства. Легко видеть, что если даны значения этих коэффициентов во всех точках пространства (или, как сказал бы физик, задано «поле» этих коэффициентов), то возможно вычислить длину любой кривой линии, проведенной в этом неевклидовом пространстве. Все другие геометрические величины (углы, площади, объемы и т. д. ) также возможно вычислить с помощью тех же коэффициентов, которые, таким образом, приобретают первостепенное значение для геометрических свойств неевклидова пространства. Ими, как говорят, определяется «метрика» пространства, т. е. результаты всех производимых в нем измерений. Коэффициенты эти получили довольно громоздкое название «компонентов метрического фундаментального тензора». Понятно, что вся суть заключается именно в этих компонентах. Если между двумя точками проведены две кривые линии, то, например, вопрос о том, которая из них короче, может быть решен только в том случае, если заданы значения компонентов метрического фундаментального тензора в каждой точке. Линия, которая не оказалась бы кратчайшим расстоянием между двумя точками в пространстве евклидовом, где все компоненты метрического фундаментального тензора равны или нулю или единице, может оказаться кратчайшей линией, если задано какое-нибудь другое распределение этих компонентов в пространстве, соответствующее неевклидовой геометрии.

Идея Эйнштейна, примененная им к изучению

248

 

полей тяготения, заключалась в том, что четырехмерная пространственно-временная совокупность точек-событий не должна обязательно являться евклидовой, а может быть и неевклидовой. Если в какой-нибудь области пространства отсутствует поле тяготения, то согласно Эйнштейну геометрия четырехмерной пространственно-временной совокупности может считаться евклидовой. В этом случае материальная точка, на которую не действуют электромагнитные силы (т. е. не действуют никакие силы вообще, так как, кроме сил тяготения, все известные в физике силы сведены к электромагнитным), то рассматриваемая точка будет двигаться согласно закону инерции равномерно и прямолинейно.

До Эйнштейна полагали, что роль сил тяготения принципиально не отличается от роли электромагнитных сил, т. е. что действие тех и других сил состоит в сбивании материальной точки с того кратчайшего пути, по которому она двигалась бы в отсутствие сил. Эйнштейн решил этот вопрос совершенно новым и неожиданным образом. Если под силами подразумевать те причины, по которым график движения материальной точки перестает быть кратчайшей или прямейшей линией, то загадка сил тяготения получает следующее парадоксальное разрешение: сил тяготения вообще не существует! существует только свойство тяжелых тел создавать вокруг себя такие неевклидовы свойства пространства, такое, как говорят, «искривление» пространства, благодаря которому материальная точка движется в отсутствие электромагнитных сил не по тем линиям, по каким она бы двигалась в случае евклидовой метрики, а по другим.

Из предыдущего ясно, что поле тяготения является в эйнштейновой теории геометрическим свойством пространства, поскольку оно может быть вычислено по значениям тех коэффициентов, которыми определяется длина проведенных в четырехмерном пространстве Эйнштейна—Минковского кривых линий. Заслуга Эйнштейна заключается в том, что он нашел закон, которому должно удовлетворять поле этих метрических коэффициентов в четырехмерном пространстве («закон тяготения Эйнштейна»). Роль материи сводится к тому только, что присутствие материи вызывает искривление пространства и нарушение первоначальных евклидовых его свойств. Отсюда ясно, что в теории относительно-

249

 

сти Эйнштейна электромагнитные силы и силы тяготения играют принципиально различную роль: силы тяготения вытекают непосредственно из геометрических свойств четырехмерной пространственно-временной совокупности точек-событий, между тем как электромагнитные силы не имеют ничего общего с геометрией и не могут быть вычислены по заданным значениям компонентов метрического фундаментального тензора.

Такое различие между электромагнитными и гравитационными силами считалось недостатком теории, и многие исследователи пытались создать такую теорию электромагнитного поля, в которой электрические и магнитные величины вычислялись бы из геометрических свойств пространства-времени. Одной из попыток такого рода является теория Калуцы (1921 г. ). Вместо четырехмерной совокупности точек Калуца рассматривал пятимерную, в которой число метрических коэффициентов было поэтому больше, чем в четырехмерной совокупности. Потенциалы электромагнитного поля вычислялись им из этих коэффициентов. Теория Калуцы не имела успеха, хотя его идеи сыграли некоторую роль (пятимерная совокупность точек была снова введена в 1927 г. немецким математиком Оскаром Клейном и русским математиком В. А. Фоком в их математическом истолковании волновой механики Шредингера). К другим попыткам свести электромагнитное поле к геометрическим свойствам пространственно-временного мира принадлежит теория, разработанная цюрихским математиком Германом Вейлем. Эта теория также не смогла удовлетворительно описать электромагнитные явления, как и теория Калуцы. Обе теории удовлетворительно справлялись с уравнениями электромагнитного поля в пустоте, но не могли объяснить законов движения материи в этом поле.

Теория Эйнштейна, о которой идет речь в этой заметке, ставит перед собой такую же самую цель — включение электромагнитного поля в систему чисто геометрических величин. Для того чтобы понять новую теорию Эйнштейна, названную им «единой теорией поля», нужно рассмотреть понятие о параллелизме в неевклидовой геометрии. Пусть в неевклидовом пространстве дана точка 1 и в ней задано некоторое направление (например, направление некоторого бесконечно малого отрезка, начинающегося в точке 1). Пусть через точку 2 того же неевклидового пространства тре-

250

 

буется провести отрезок, параллельный заданному бесконечно малому отрезку в точке 1. Простейшим способом является следующий. Соединим точки 1 и 2 геодезической (кратчайшей) линией и будем перемещать вдоль этой линии бесконечно малый отрезок из точки 1 в точку 2 так, чтобы при каждом бесконечно малом перемещении, на которые можно разложить его путь от точки 1 к точке 2, он оставался параллелен самому себе. Ясно, что, придя в точку 2, он будет находиться под тем же углом к касательной, проведенной к геодезической линии, под которым он находился в точке 1. На первый взгляд может казаться, что то положение, которое отрезок принял в точке 2, можно считать параллельным его первоначальному направлению в точке 1. Однако с этим связаны трудности. Если, например, дана, кроме точек 1 и 2, еще и точка 3, то можно было бы переместить бесконечно малый отрезок параллельно самому себе сперва из точки 1 к точке 3 по соединяющей их геодезической линии, а затем из точки 3 к точке 2 по геодезической линии 3 2. Окажется, что после двух таких перемещений бесконечно малый отрезок будет занимать в точке 2 не то положение, какое он имел бы при непосредственном перемещении параллельно самому себе по геодезической линии 1 2, а другое.

Таким образом, понятие параллелизма не может быть обобщено на пространство, обладающее кривизной. Это можно проверить на простом случае шаровой поверхности, которую можно рассматривать, как двумерное неевклидово пространство. Пусть на поверхности шара даны три точки 1, 2 и 3. Соединим их попарно дугами больших кругов (известно, что на поверхности шара дуга большого круга, соединяющая две точки, является кратчайшим расстоянием между ними). Получился сферический треугольник 123. Если в точке 1 проведен какой-нибудь отрезок в касательной плоскости к шару, то его можно переместить вдоль стороны сферического треугольника 1 2 таким образом, чтобы он все время оставался касателен к шару и все время образовывал один и тот же угол с касательной к большому кругу 1 2. Это и будет «перемещение параллельно самому себе» по геодезической линии 1 2. После этого его можно таким же образом «перенести параллельно самому себе» по геодезической линии 2 3, а затем и по линии 3 1. Окажется, что

251

 

после такого «перемещения параллельно самому себе» по контуру сферического треугольника 123 отрезок не придет в прежнее положение, а образует со своим первоначальным направлением в точке 1 некоторый угол. С помощью элементарной геометрии нетрудно доказать, что этот угол будет равен так называемому «сферическому эксцессу» треугольника 1 2 3, т. е. разности между суммой углов сферического треугольника 1 2 3 и 180 градусами. (Сферический эксцесс треугольника, как доказывается в сферической тригонометрии, пропорционален площади треугольника. ) Из этого примера видно, что сохранить на поверхности шара понятие о параллелизме без добавочных условий невозможно.

Новая теория Эйнштейна вводит в неевклидову геометрию понятие о параллелизме следующим образом: в каждой точке четырехмерного пространства проводятся четыре взаимно перпендикулярные направления, образующие в каждой точке как бы систему прямоугольных осей. Про эти оси вводится допущение, что они в разных точках пространства параллельны друг другу. Нетрудно видеть, что для определения положения этих четырех осей необходимо задать в каждой точке значения шести величин, из которых первые три определяют положение первой оси, вторые две — положение второй оси, наконец последняя определяет положение третьей оси, для определения же четвертой оси не нужно задавать добавочных величин, так как достаточно того, что она перпендикулярна остальным осям. Между ними устанавливает Эйнштейн ряд соотношений, которые вводятся для того, чтобы придать понятию о параллелизме определенный смысл и которые, кроме того, должны удовлетворять так называемому «требованию ковариантности». Это требование значит, что соотношения должны иметь одинаковую форму независимо от той координатной системы, с которой связан измеряющий геометрические свойства пространственно-временной совокупности наблюдатель. Требование ковариантности вообще играет основную роль в теории относительности. Оказывается, что выведенным для этих шести величин соотношениям возможно придать другую форму, а именно: определенные комбинации из этих величин возможно назвать (совершенно условно) слагающими электромагнитных сил и сил тяготения. Тогда окажется, что упомянутые соотно-

252

 

шения превратятся в такие соотношения между электромагнитными и гравитационными силами, которые совершенно удовлетворительно оправдываются на опыте в случае пустого пространства. В этом заключается важнейший результат новой теории Эйнштейна. Отсюда видно, что электромагнитные силы уже не противопоставляются гравитационным, как это было в общей теории относительности Эйнштейна. Электромагнитные силы, как и силы тяготения, оказываются геометрическими характеристиками четырехмерной пространственно-временной протяженности.

В этом монистическом характере, позволяющем связать геометрию, тяготение и электричество в одно единое целое, заключается главное достоинство новой теории Эйнштейна. Эта теория приводит, таким образом, к своеобразному физическому мировоззрению, о построении которого уже несколько столетий назад мечтал знаменитый французский философ и математик Ренэ Декарт.

Следует сказать, однако, что теория Эйнштейна еще не построена до конца. Так, например, еще не решен вопрос о графиках движения материальных частиц в четырехмерной протяженности точек-событий под влиянием электромагнитных и гравитационных сил. Остается невыясненным, удастся ли на основании новой теории Эйнштейна вывести существование двух противоположных родов электричества и сделать, таким образом, шаг вперед по сравнению с теорией Германа Вейля. Точно так же остается решить вопрос об отношении новой теории Эйнштейна к теории квантов. Прерывный характер явлений, происходящих в чрезвычайно малых объемах, занятых отдельными атомами вещества, указывает с большой вероятностью на то, что эта прерывность должна найти свое отражение в геометрии, и что, таким образом, свойства пространственно-временной протяженности должны иметь квантовый, прерывный характер. Построение такой геометрии пространства и времени, из которой вытекали бы не только законы тяготения и электромагнитного поля, но и квантовые законы,— вот величайшая задача, которая когда-либо стояла перед физикой.

 

Эфир и его роль в старой и новой физике

Человек и природа. 1929. № 16, С. 3-9. 

 

Судьбы физических теорий, как судьбы людей, пестры и разнообразны. Они отличаются друг от друга и продолжительностью жизни, и быстротой, с которой им удается занять в науке прочное положение, и широтой охватываемой ими области физических явлений, и упорством, с которым они отстаивают свое существование под напором новых, настойчиво требующих истолкования фактов. Но из всех теоретических построений физики вряд ли найдется хотя бы одно, которому выпало на долю больше странных и неожиданных превратностей, чем гипотезе эфира — одной из древнейших и важнейших физических гипотез. Эфир, как Протей, принимал всевозможные формы, подчинял своему владычеству все новые и новые области физики, расцветал и снова хирел (один раз был даже вовсе «упразднен»), одному поколению казался «более реальным, чем вода и воздух», а другому — «старым хламом, который нужно сдать в архив, как сданы туда флогистон и теплород». Каждая эпоха в истории физики имела свой особенный эфир; и от столетия к столетию эфир проносил неизменным только свое мистически звучащее имя и неограниченную претензию быть основным субстратом более или менее всеобъемлющей группы физических явлений.

Эфир родился в блестящих, хотя и не всегда научных спекуляциях философов античной Греции. В эти дни своей молодости эфир не исполнял никаких специальных обязанностей: не было ни одной конкретной области физических явлений, которую бы он был призван объяснять. Но он был нужен, как «пятая стихия», которую необходимо было добавить к известным четырем (земля, вода, воздух и огонь), чтобы иметь возможность производить их от общего корня и тем самым внести мнимую простоту в подавляющую сложность явлений внешнего мира.

Таким «философским эфиром» античный эфир оставался очень долго, и даже еще для Ньютона суще-

254

 

ствование эфира было скорее философской аксиомой, чем физической теорией. Пресловутое «действие на расстоянии», т. е. возможность для тела вызывать своим присутствием, без помощи промежуточной среды, действие сил в точках пространства, в которых само тело не находится, претило здравому смыслу Ньютона в такой же мере, как и философскому гению Декарта и Лейбница. Вот почему Ньютон протестовал против такой возможности, столь любезной епископу Беркли, и считал ее философски нелепой, полагая, что все такие мнимые «действия на расстоянии» (тяготение, взаимодействия намагниченных или наэлектризованных тел) должны в конечном счете объясняться действием промежуточной среды, которую он называл эфиром. Но, по мнению Ньютона, было еще слишком рано заниматься рассмотрением механизма такой передачи действия через эфирную среду, как это делал, например, Декарт, объяснявший движение планет увлекающим их эфирным вихрем. Поэтому Ньютон ограничивался математическим описанием «действий на расстоянии» и, допуская существование эфира, «не придумывал гипотез» о его физической природе.

Совершенно иначе относился к гипотезе эфира гениальный современник Ньютона Христиан Гюйгенс, который дал эфиру специальную физическую службу, заставив его объяснять оптические явления. Созданная Гюйгенсом гипотеза «светового эфира», мыслившегося в виде упругой материальной среды, через которую могут проноситься волны сжатия и разрежения, воспринимаемые нами, как световые явления, вела больше столетия неравную борьбу с ньютоновской корпускулярной теорией света (гипотезой истечения).

Только во второй четверти XIX в., после того как Юнг и Френель исследовали целый ряд явлений (интерференция, дифракция, поляризация света), легко объясняемых гипотезой о волнах в эфире, но почти не поддающихся истолкованию на почве гипотезы истечения, теория упругого светового эфира восторжествовала над своей соперницей (окончательным торжеством теории волн был опыт Физо, измерившего скорость света в воде и нашедшего, что она, в противность теории истечения, меньше, чем в воздухе). При этом пришлось отказаться от предположения Гюйгенса, что волны света суть продольные волны разрежения и сжатия, вполне аналогичные волнам, распространяю-

255

 

щимся в газообразных телах (например, звуковым волнам); явления поляризации света могли быть объяснены лишь допущением, что световые волны являются поперечными волнами, как те поперечные упругие волны, какие могут распространяться лишь в телах, сопротивляющихся изменению своей формы, т. е. в упругих твердых телах.

Так возникла теория «твердого» эфира — чрезвычайно разреженной и вместе с тем необыкновенно упругой твердой среды, заполняющей все пространство Вселенной и пронизывающей все промежутки между атомами тел, оказывая при этом лишь самое ничтожное и не поддающееся измерению сопротивление движению этих тел. Построенная на этих предположениях «механическая теория света» является одним из наиболее глубокомысленных созданий человеческого гения; но и она оказалась бессильной справиться с вставшими перед ней затруднениями.

Первое из таких затруднений заключалось в следующем: обычные упругие твердые тела сопротивляются не только изменению своей формы, но также и изменению объема. Поэтому через них могут распространяться не только, поперечные волны, но и продольные волны сжатия и разрежения, как в жидкостях и газах. Возникает вопрос: почему в световом эфире не наблюдаются явления, соответствующие распространению продольных воли? Помешать такому распространению могли бы только два обстоятельства: или эфир не обладает никакой упругостью по отношению к изменениям объема, т. е. при его сжатии или разрежении в нем вовсе не возникают силы, сопротивляющиеся такому сжатию или разрежению; или же в эфире никакие сжатия или разрежения вообще невозможны. Первое предположение соответствует беспредельно сжимаемому эфиру, второе — абсолютно несжимаемому.

Теорией абсолютно несжимаемого эфира занимался английский математик Джордж Грин. Получить наглядное представление об эфире Грина возможно, сравнив его с каким-либо твердым телом, у которого сопротивление изменению объема чрезвычайно велико по сравнению с сопротивлением изменению формы. Таков, например, каучук или в особенности желатина. Несжимаемый эфир Грина соответствует предельному случаю бесконечно большой скорости распространения про-

256

 

дольных колебаний. Теория Грина встретила ряд возражений. В частности, оказалось, что эта теория приводит к расходящемуся с опытом результату в вопросе об изменении интенсивности и состояния поляризации в отраженных и преломленных лучах по сравнению с лучами падающими.

Поэтому в 80-х годах прошлого века лорд Кельвин разработал теорию беспредельно сжимаемого эфира (вторую из упомянутых возможностей). И в этой теории встречаются серьезные затруднения. Важнейшим является то, что эфир, не оказывающий никакого сопротивления сжатию, должен быть механически неустойчив. Такая неустойчивость могла бы быть устранена, если предположить, что эфир неподвижно укреплен на каких-то границах. Простейшую модель такого эфира представляла бы пена, заключенная в сосуде, к стенкам которого она прилипает и который не содержит воздуха. Однако трудно предположить, чтобы в природе могло быть нечто вроде гигантского ящика, заключающего всю звездную Вселенную, к стенкам которого неподвижно прикреплен эфир. Поэтому и эфир Кельвина, соответствующий предельному случаю бесконечно малой скорости продольных волн, тоже не может считаться удовлетворительным средством механического объяснения световых явлений. Насколько неопределенными были взгляды самого Кельвина на этот вопрос, показывает то обстоятельство, что наряду с теорией упругого твердого, беспредельно сжимаемого эфира он разрабатывал также вихревую теорию атомов, согласно которой атомы вещества представляют собой вихри в некоторой среде, называемой им эфиром и обладающей свойствами не упругого твердого тела, а идеальной (т. е. лишенной вязкости) жидкости. Свойства вихревых колец в идеальной жидкости были математически исследованы Гельмгольцем, который показал, например, что такие вихри, раз образовавшись, не могут уничтожиться (что, по Кельвину, представляет истинный смысл закона сохранения вещества).

Разумеется, эфиру было очень трудно справляться сразу с таким количеством обязанностей (объяснение световых явлений, объяснение свойств атомов), тем более, что со времен Фарадея (т. е. с середины прошлого века) на обязанности эфира лежало также механическое истолкование обширнейшей области электри-

257

 

ческих и магнитных явлений. Когда Клерк Максвелл «перевел взгляды Фарадея на математический язык», на основе его математической теории выросла «электромагнитная теория света», трактовавшая свет как переменное электромагнитное поле. Важнейшие свойства световых явлений смогли быть выведены из уравнений электромагнетизма («уравнений Максвелла»), и с тех пор различные задачи объяснения оптических и электромагнитных явлений стали одной и той же задачей. В своем знаменитом «Трактате об электричестве и магнетизме» Максвелл показал, что в известных пределах возможно обойтись и без детальной модели эфира, сделав лишь несколько общих предположений о механической природе электромагнитных явлений. Важнейшим является то, что электрическая энергия считается потенциальной энергией упругих деформаций эфира, а магнитная энергия — кинетической энергией происходящих в эфире движений. Это соответствует и предположению Фарадея, считавшего электрическое поле системой натяжений в эфире, а магнитное поле — системой вихревых движений.

Такой эфир, по мысли Максвелла, может рассматриваться, как механизм со скрытыми частями. Это значит, что не все величины, определяющие собой расположение частей механизма, могут быть наблюдены или измерены. Некоторые из этих величин, называемых условно «координатами» механизма, доступны измерению, другие измерению недоступны, но зато у некоторых из этих последних может быть измерена быстрота их изменения во времени. Максвелл полагал, что механизм эфира обладает свойствами, позволяющими в ряде случаев изучать с помощью обычной механики законы изменения во времени доступных измерению величин (т. е. законы движения явных частей механизма), не зная ничего о скрытых его частях.

Максвелл предлагает такую аналогию: пусть имеется какая-то машина в запертой комнате, соединенная с веревками, концы которых свешиваются через отверстия в полу в другую комнату в нижнем этаже. Человек, вошедший в нижний этаж, не может видеть самой машины, но, дергая за одну из веревок, замечает, что и другие веревки при этом приходят в движение; отсюда он заключает о существовании какого-то соединяющего их механизма. Скрытые части этого механизма недоступны его наблюдению, но он в состоянии

258

 

прийти к некоторым выводам относительно веревок (которые можно трактовать, как явные части того же самого механизма), если только он допустит, что скрытые части подчиняются законам механики. Так, например, он находит из опыта, что при опускании конца веревки А на один дюйм, конец веревки Б поднимается на два дюйма. Механизм, соединяющий веревки А и Б, может быть различен (это мог бы быть рычаг, или блок, или даже часовой механизм), но если только он подчиняется законам механики, то можно заранее сказать, что груз, подвешенный к веревке А, может быть уравновешен вдвое меньшим грузом, подвешенным к веревке Б (это следствие основного закона статики — так называемого «начала возможных перемещений»).

Уравнения электромагнитного поля также трактовались Максвеллом как результат применения законов механики к эфирному механизму, многие части которого скрыты. Одно время могло казаться, что такой способ трактовки электромагнитных явлений обещает много плодотворных результатов, но через некоторое время разразился кризис, разрешившийся уже только в начале нынешнего столетия.

Этот кризис, из которого эфир вышел потерявшим свою материальную природу (а по мнению некоторых, даже и вовсе не вышел живым), возник в связи с изучением электромагнитных (и в том числе оптических) явлений в движущихся телах. Задача, которая привела к такому кризису, заключалась в определении той скорости, с которой наша планета движется сквозь предполагаемую эфирную среду. Принципиальная возможность определения этой скорости вытекает из того обстоятельства, что если эфир представляет материальную среду, то электромагнитные и оптические свойства тела, движущегося сквозь эту среду, не могут быть по всем направлениям одинаковыми.

Представим себе утку, плывущую по поверхности пруда и периодически ударяющую по поверхности воды лапкой. От лапки во все стороны по воде бегут волны. Эти волны представляют собой бегущие по воде круги, но ясно, что сама утка не будет в центре такого круга. В самом деле, пока вызванное ударом утиной лапки волнение дойдет до окружности круга, утка успеет передвинуться на некоторое расстояние и будет поэтому ближе к одному краю круга, чем к дру-

259

 

гому. Это значит, что перемещающийся гребень волн будет по одному направлению дальше отстоять от утки, чем по другому, т. е. что скорость распространения волны относительно утки будет по одному направлению иная, чем по другому. Это заключение основано на том, что утка перемещается относительно воды, а не увлекает ее с собою, и на том, что волнение, вызванное движущейся уткой, распространяется по поверхности воды с такой же скоростью, как если бы утка была неподвижна. Если удастся оба эти положения распространить и на световые волны (источник света играет роль утки), то можно было бы утверждать, что скорость света от движущегося источника, измеренная по отношению к этому источнику, должна быть различна по разным направлениям. Посмотрим, можно ли в самом деле распространить эти утверждения на эфир. Увлекается ли эфир движущимися телами? Иными словами, прибавляется ли к скорости света, распространяющегося в движущейся среде, скорость этой среды? Этот вопрос был исследован еще Френелем, который вывел теоретически, что к скорости света, распространяющегося в движущейся среде, прибавляется не вся скорость среды, а часть ее, зависящая от показателя преломления этой среды. Если показатель преломления равен единице, что практически имеет место для воздуха, то прибавляющаяся к скорости света часть скорости среды обращается в нуль, т. е. эфир в этом случае не увлекается вовсе. Справедливость формулы Френеля проверил на опыте Физо, который измерял скорость света в движущейся воде (подразумевается скорость света не по отношению к воде, а по отношению к источнику света, находящемуся вне струи воды, т. е. неподвижному). Вывод Френеля может быть подтвержден также из рассмотрения явления аберрации света, т. е. кажущегося смещения неподвижных звезд к той точке небесного свода, куда в данный момент направлена скорость движения Земли вокруг Солнца. Для телескопа, наполненного воздухом, справедливость формулы Френеля подтверждается астрономами, так сказать, еженощно; для телескопа же, наполненного водой, формула Френеля была подтверждена лишь в 1871 г. английским физиком Эйри. Так как в дальнейшем мы предполагаем распространение света в воздухе, то можем считать, что эфир при движении не увлекается.

260

 

Второй вопрос, который нужно решить, чтобы знать, имеем ли мы право применять к оптическим явлениям то, что выше было выведено для случая плывущей утки, состоит в том, зависит ли от движения источника скорость его света, измеренная по отношению к среде, относительно которой источник движется. Волновая теория света отвечает на этот вопрос отрицательно, но окончательным судьей может быть только физический опыт или астрономическое наблюдение. Ведь волновая теория света в конце концов не является обязательным догматом, и еще в этом столетии швейцарский физик В. Ритц предлагал так называемую «баллистическую гипотезу», согласно которой скорость источника прибавляется к скорости света для луча, вышедшего по направлению движения источника, и вычитается в случае обратного направления (баллистической гипотеза называется потому, что таким же точно образом влияет скорость движения артиллерийского орудия на скорость вылетающего из него снаряда). Гипотеза Ритца была опровергнута голландским астрономом де Ситтером, который указал на то, что в случае ее справедливости происходило бы кажущееся вытягивание орбит двойных звезд по направлению к Земле, вследствие чего большие полуоси этих орбит были бы направлены преимущественно к Земле, чего в действительности не наблюдается. Из этой работы де Ситтера и из некоторых других работ можно сделать заключение: скорость источника света не влияет на скорость распространения света в эфире. Таким образом, верно и то заключение, о котором мы сказали выше: скорость света, измеренная на движущейся Земле, должна быть разной по разным направлениям, и изучение этой скорости в различных направлениях позволит решить вопрос о направлении и величине скорости движения Земли сквозь эфир. Это верно в том случае, если эфирная среда представляет материальный океан, так что вообще имеет смысл говорить о перемещении Земли по отношению к такому океану.

Измерение скорости света в различных направлениях было осуществлено в знаменитом опыте Майкельсона (1881 г. ). Здесь не место входить в детали описания этого опыта, тем более, что он общеизвестен; для нас важно лишь то, что из этого опыта вытекает равенство скорости света по всем направлениям, что противоречит сделанному выше выводу и делает не-

261

 

возможным обнаружение таким способом скорости Земли по отношению к эфиру. Другие попытки обнаружить эту скорость также кончились неудачей: из них назовем опыт Рэлея и Брэса, в котором нужно было обнаружить вытекавшее из теории двойное лучепреломление в воде, стекле и сероуглероде, вызванное движением Земли сквозь эфир (никакого двойного лучепреломления в действительности не наблюдалось); затем опыт Траутона и Рэнкина, которые так же тщетно пытались обнаружить другой предсказываемый теорией эффект движения Земли сквозь эфир, а именно изменение электрического сопротивления проволоки при изменении ее направления относительно направления предполагаемой скорости Земли; наконец опыт Траутона и Нобля, пытавшихся измерить скорость движения Земли сквозь эфир по тем силам, которые это движение должны вызвать в электрическом конденсаторе.

Все опыты, а также построенный на их основании Эйнштейном специальный принцип относительности приводят к заключению: скорость движения Земли сквозь эфир измерена быть не может, как будто все силы природы вступили между собой в заговор — скрыть от физиков величину и направление этой скорости. Итак тело, покоящееся в эфире, никакими способами не может быть отличено от тела, движущегося в нем. Но это бессмысленно, если эфир представляет материальную среду, части которой могут быть отличены друг от друга; движение относительно материальной среды не может быть эквивалентно покою в ней. Не желая, по-видимому, иметь дело с лишенным общеизвестных свойств материи эфиром, физики сделали вывод (по крайней мере, большинство из них), что эфира не существует вовсе! и что раз он не может быть найден из опыта (точней, не самый эфир, а покой в нем), то нет никакого смысла о нем говорить. По мнению Борна, это было началом того гонения на «принципиально ненаблюдаемые величины», которое в современной физике привело к созданию «матричной механики» Гейзенберга, Борна и Йордана и к тому, что физика теперь не решается говорить о такой, например, величине, как расстояние электрона до ядра в атоме (ибо расстояние для современного физика есть то, что измеряется линейкой, а даже сам тульский левша, который «аглицкую блоху на подковы подко-

262

 

вал», не умудрится приготовить линейку для измерения расстояния электрона до ядра в атоме).

Такова была смерть эфира, случившаяся в первое десятилетие этого века; но рассказ о нем не кончается на этом. Как Юлий Цезарь в шекспировской трагедии, убитый физически в третьем акте, остается тем не менее героем остальных двух и его убийца Брут вынужден разговаривать с его бесплотным призраком, так и эфир, как оказалось впоследствии, был убит лишь «физически», но остался одним из героев физики, и даже Эйнштейн, главнейший его убийца, должен был вступить в переговоры с привидением (см., например, его лейденскую речь «Эфир и принцип относительности», 1920 г., есть и русский перевод).

Случилось это следующим образом: дальнейшее развитие принципа относительности привело к «общей теории относительности», представляющей нечто вроде геометрии пространства и времени, в которой чисто физические величины, такие, как силы тяготения, выводятся из геометрических величии (из десяти так называемых «компонент метрического фундаментального тензора», значение которых задается в каждом точечном «событии», т. е. в каждой точке пространства в каждый момент времени). В новейшей форме теории относительности (в так называемой «единой теории поля») вместо 10 геометрических величин вводится 16, из которых зато могут быть вычислены не только силы тяготения, но и электромагнитные силы. Но ясно, что физические величины не могли бы быть выведены из геометрических, если бы уже каким-то образом не заключались в них; и если физика становится геометрией пространства и времени, то эта геометрия в такой же мере становится физикой. Пространство, которое обладает геометрическими свойствами, влияющими на материю и в свою очередь обусловленными этой материей, уже перестает быть пространством просто, а становится чем-то большим, чем пространство, т. е. средой (хотя бы и не материальной). Нельзя удивляться тому, что эта среда получила название эфира. Как ни мало общего у этого нового эфира с упругим твердым эфиром Юнга и Френеля, все же он по-прежнему является носителем световых (а также и вообще электромагнитных) явлений, причем вместе с тем он объясняет и явления тяготения.

Отрицать эфир, по словам Эйнштейна, значило бы

263

 

допускать, что пустое пространство не имеет никаких физических свойств. В действительности оно обладает большим количеством свойств (если судить по тому, что для их описания единая теория поля употребляет 16 функций); но не следует только представлять его, себе состоящим из частей, по отношению к которым имеет смысл понятие движения. Эйнштейн по этому поводу говорит следующее: «Называемое "пустым" пространство в физическом отношении ни однородно, ни изотропно: мы вынуждены описывать его состояние с помощью десяти функций — гравитационных потенциалов. Но, таким образом, и понятие эфира снова приобретает определенное содержание, которое совершенно отлично от содержания понятия эфира механической колебательной теории. Эфир всеобщей теории относительности есть среда, сама по себе лишенная всех механических и кинематических свойств, но в то же время определяющая механические и электромагнитные события».

Примерно так же высказывается об эфире и Эддингтон (в его последней книге «Природа физического мира», Кембридж, 1928 г., русского перевода нет). Эддингтон говорит: «Нельзя думать, что эфир упразднен. Эфир нам нужен. Физический мир не может быть разложен на изолированные частицы материи или электричества, пространство между которыми лишено всяких свойств. Этому "пустому" пространству приходится приписывать так же много свойств, как и самим частицам, и современной физике понадобилась целая армия математических символов, чтобы описать, что происходит в пустом пространстве. Мы постулируем, что эфир обладает свойствами этого пространства, как материя или электричество — свойствами частиц. . . В прошлом столетии было широко распространено мнение, что эфир представляет нечто вроде материи, обладая массой, твердостью, движением, как и обычная материя. . . Теперь решено, что эфир не является чем-то вроде материи. Не будучи материальным, он обладает свойствами совершенно другого рода. Эти свойства должны быть найдены из опыта».

Эфир подобного рода отличается, конечно, высокой степенью эластичности — не в том смысле, в каком это слово могло бы употребляться в теории Юнга и Френеля, а в том, что такой эфир не обязался удовлетворять ни одному предвзятому мнению, и опыт в со-

264

 

стоянии только изменить о нем представления, но не упразднить его существование. После того как ему случилось один раз умереть, он стал отличаться необыкновенной живучестью. В конце концов спор о существовании эфира становится спором о словах, вроде известной дискуссии между китайскими учеными и иезуитскими миссионерами о том, в какую сторону указывает магнитная стрелка, на юг или на север. Но никто не в состоянии воспрепятствовать физикам употреблять ту терминологию, какая им удобна, поэтому физики и будут пользоваться понятием эфира, хотя и значительно, как мы видели, отличным от того, что подразумевалось под эфиром в прошлом столетии.

 

---

Оглавление

Предисловие. 5
Глава 1. Детство и юность. Путь в науку. Первые научные работы   12
Глава 2. В Ленинградском университете (1926-1930 гг. ) 26
Глава 3. В Ленинградском  физико-техническом институте  57
Глава 4. О трудных временах для законов сохранения и о трудной профессии физика-теоретика  125
Глава 5. cGћ-физика в биографии Бронштейна. 169
Глава 6. Стиль творческой личности. 244
Библиография. 294
Приложение. Две статьи М. П. Бронштейна из журнала «Человек и природа» за 1929 год  312